Nonlocal Retinex-Based Variational Model and its Deep Unfolding Twin for Low-Light Image Enhancement

Images captured under low-light conditions present significant limitations in many applications, as poor lighting can obscure details, reduce contrast, and hide noise. Removing the illumination effects and enhancing the quality of such images is crucial for many tasks, such as image segmentation and object detection. In this paper, we propose a variational method for low-light image enhancement based on the Retinex decomposition into illumination, reflectance, and noise components. A color correction pre-processing step is applied to the low-light image, which is then used as the observed input in the decomposition. Moreover, our model integrates a novel nonlocal gradient-type fidelity term designed to preserve structural details. Additionally, we propose an automatic gamma correction module. Building on the proposed variational approach, we extend the model by introducing its deep unfolding counterpart, in which the proximal operators are replaced with learnable networks. We propose cross-attention mechanisms to capture long-range dependencies in both the nonlocal prior of the reflectance and the nonlocal gradient-based constraint. Experimental results demonstrate that both methods compare favorably with several recent and state-of-the-art techniques across different datasets. In particular, despite not relying on learning strategies, the variational model outperforms most deep learning approaches both visually and in terms of quality metrics.

A Survey of Pansharpening Methods with A New Band-Decoupled Variational Model

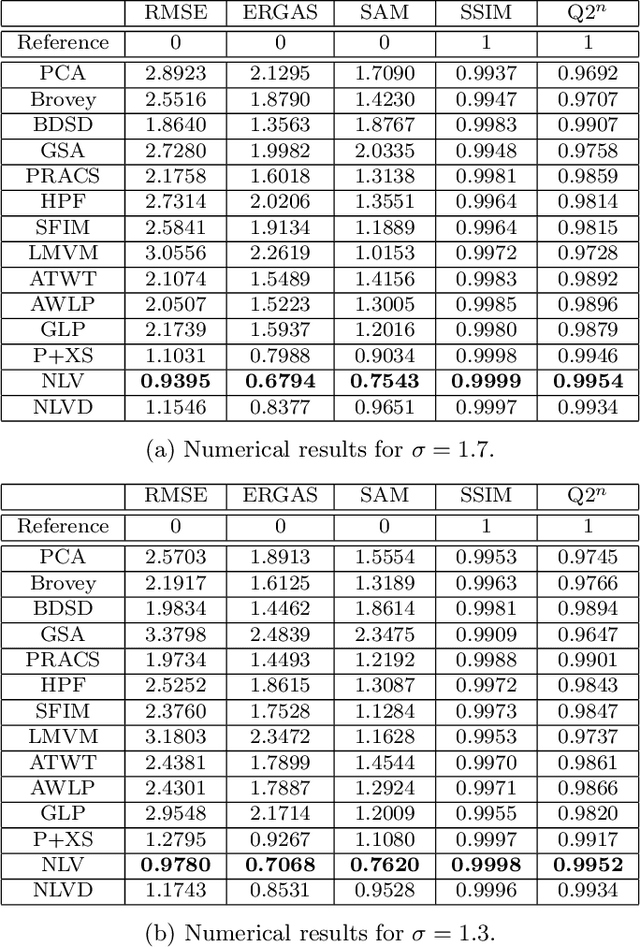
Most satellites decouple the acquisition of a panchromatic image at high spatial resolution from the acquisition of a multispectral image at lower spatial resolution. Pansharpening is a fusion technique used to increase the spatial resolution of the multispectral data while simultaneously preserving its spectral information. In this paper, we consider pansharpening as an optimization problem minimizing a cost function with a nonlocal regularization term. The energy functional which is to be minimized decouples for each band, thus permitting the application to misregistered spectral components. This requirement is achieved by dropping the, commonly used, assumption that relates the spectral and panchromatic modalities by a linear transformation. Instead, a new constraint that preserves the radiometric ratio between the panchromatic and each spectral component is introduced. An exhaustive performance comparison of the proposed fusion method with several classical and state-of-the-art pansharpening techniques illustrates its superiority in preserving spatial details, reducing color distortions, and avoiding the creation of aliasing artifacts.

Collaborative Total Variation: A General Framework for Vectorial TV Models

Even after over two decades, the total variation (TV) remains one of the most popular regularizations for image processing problems and has sparked a tremendous amount of research, particularly to move from scalar to vector-valued functions. In this paper, we consider the gradient of a color image as a three dimensional matrix or tensor with dimensions corresponding to the spatial extend, the differences to other pixels, and the spectral channels. The smoothness of this tensor is then measured by taking different norms along the different dimensions. Depending on the type of these norms one obtains very different properties of the regularization, leading to novel models for color images. We call this class of regularizations collaborative total variation (CTV). On the theoretical side, we characterize the dual norm, the subdifferential and the proximal mapping of the proposed regularizers. We further prove, with the help of the generalized concept of singular vectors, that an $\ell^{\infty}$ channel coupling makes the most prior assumptions and has the greatest potential to reduce color artifacts. Our practical contributions consist of an extensive experimental section where we compare the performance of a large number of collaborative TV methods for inverse problems like denoising, deblurring and inpainting.