Robust Guided Diffusion for Offline Black-Box Optimization

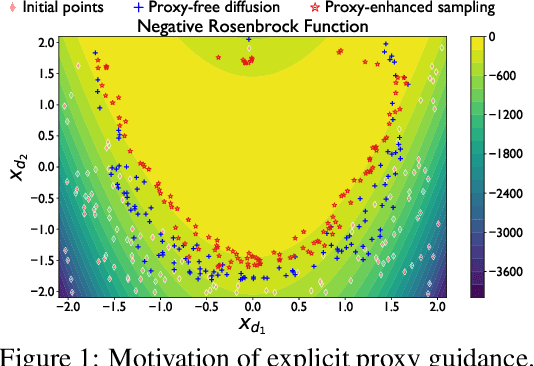
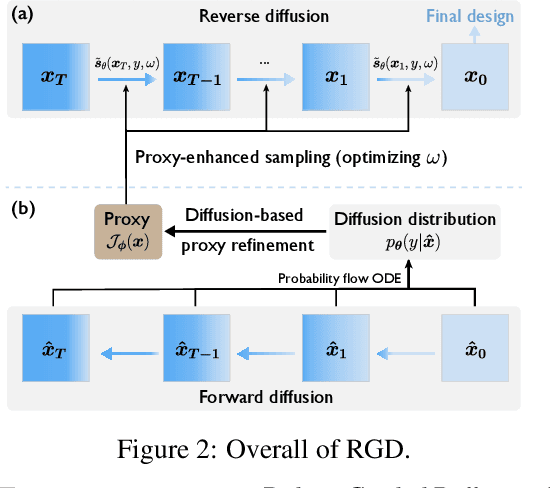
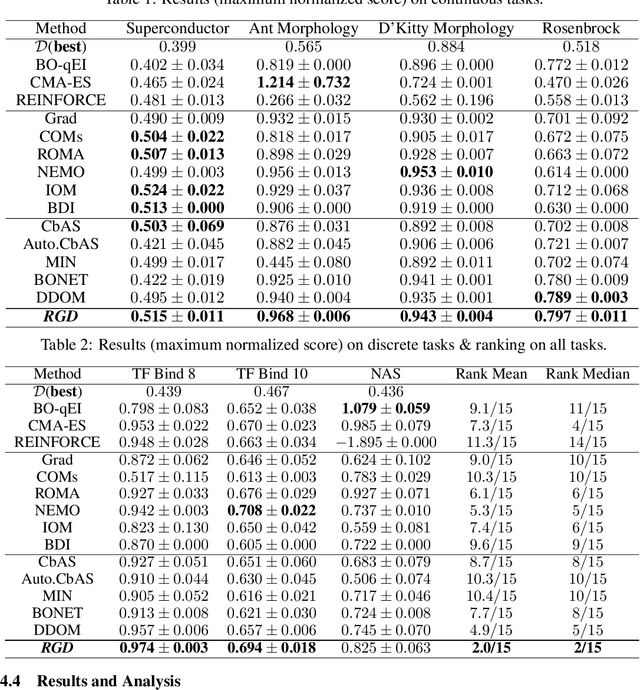
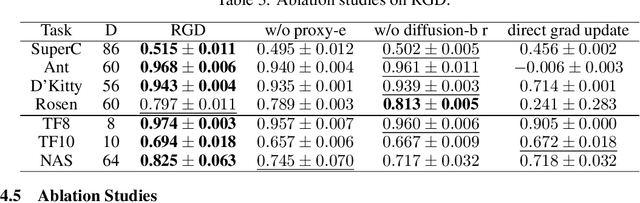
Offline black-box optimization aims to maximize a black-box function using an offline dataset of designs and their measured properties. Two main approaches have emerged: the forward approach, which learns a mapping from input to its value, thereby acting as a proxy to guide optimization, and the inverse approach, which learns a mapping from value to input for conditional generation. (a) Although proxy-free~(classifier-free) diffusion shows promise in robustly modeling the inverse mapping, it lacks explicit guidance from proxies, essential for generating high-performance samples beyond the training distribution. Therefore, we propose \textit{proxy-enhanced sampling} which utilizes the explicit guidance from a trained proxy to bolster proxy-free diffusion with enhanced sampling control. (b) Yet, the trained proxy is susceptible to out-of-distribution issues. To address this, we devise the module \textit{diffusion-based proxy refinement}, which seamlessly integrates insights from proxy-free diffusion back into the proxy for refinement. To sum up, we propose \textit{\textbf{R}obust \textbf{G}uided \textbf{D}iffusion for Offline Black-box Optimization}~(\textbf{RGD}), combining the advantages of proxy~(explicit guidance) and proxy-free diffusion~(robustness) for effective conditional generation. RGD achieves state-of-the-art results on various design-bench tasks, underscoring its efficacy. Our code is at https://anonymous.4open.science/r/RGD-27A5/README.md.

Gradient-based Bi-level Optimization for Deep Learning: A Survey

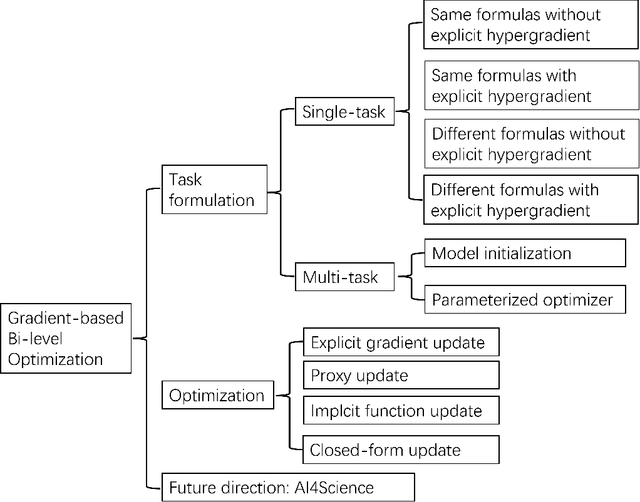
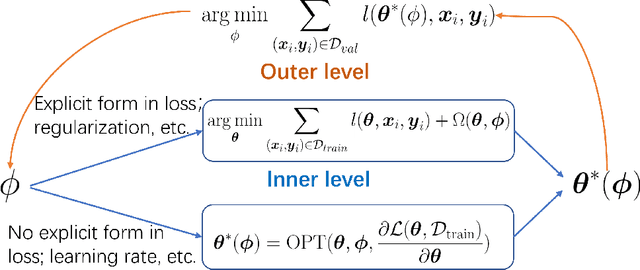
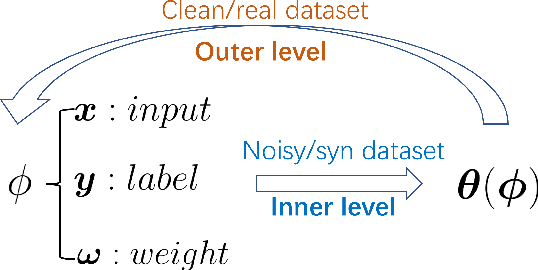
Bi-level optimization, especially the gradient-based category, has been widely used in the deep learning community including hyperparameter optimization and meta knowledge extraction. Bi-level optimization embeds one problem within another and the gradient-based category solves the outer level task by computing the hypergradient, which is much more efficient than classical methods such as the evolutionary algorithm. In this survey, we first give a formal definition of the gradient-based bi-level optimization. Secondly, we illustrate how to formulate a research problem as a bi-level optimization problem, which is of great practical use for beginners. More specifically, there are two formulations: the single-task formulation to optimize hyperparameters such as regularization parameters and the distilled data, and the multi-task formulation to extract meta knowledge such as the model initialization. With a bi-level formulation, we then discuss four bi-level optimization solvers to update the outer variable including explicit gradient update, proxy update, implicit function update, and closed-form update. Last but not least, we conclude the survey by pointing out the great potential of gradient-based bi-level optimization on science problems (AI4Science).