Brittany Terese Fasy
Vectorized Computation of Euler Characteristic Functions and Transforms
Nov 05, 2025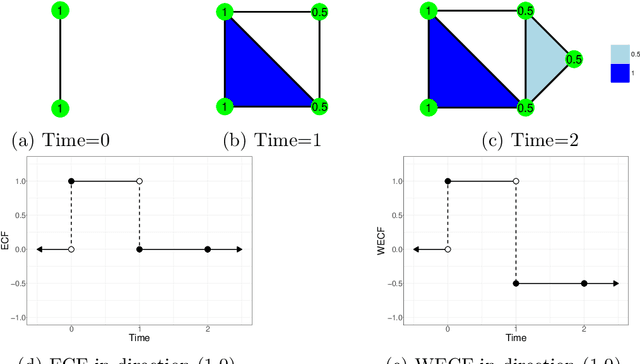
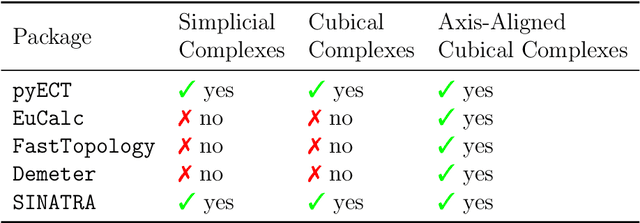
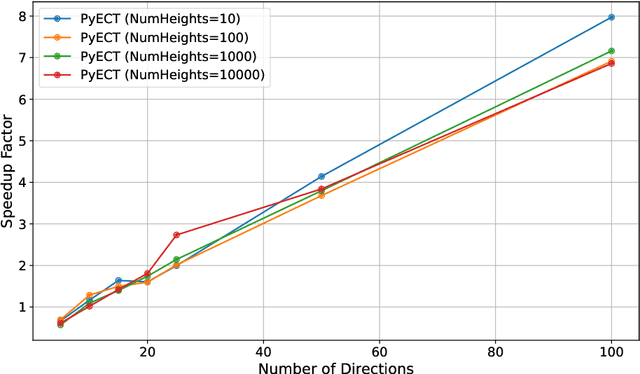
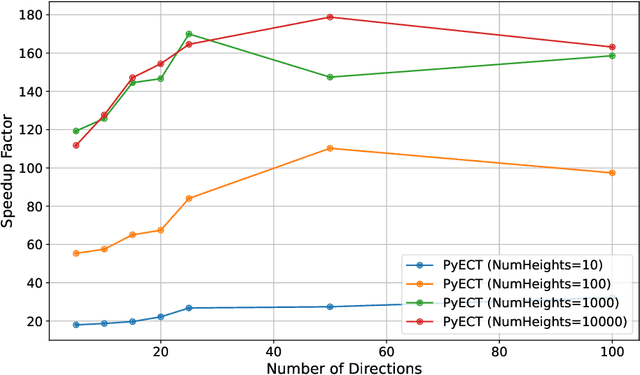
Abstract:The weighted Euler characteristic transform (WECT) and Euler characteristic function (ECF) have proven to be useful tools in a variety of applications. However, current methods for computing these functions are neither optimized for speed nor do they scale to higher-dimensional settings. In this work, we present a vectorized framework for computing such topological transforms using tensor operations, which is highly optimized for GPU architectures and works in full generality across geometric simplicial complexes (or cubical complexes) of arbitrary dimension. Experimentally, the framework demonstrates significant speedups (up to $180 \times$) over existing methods when computing the WECT and ECF across a variety of image datasets. Computation of these transforms is implemented in a publicly available Python package called pyECT.
Rapid and Precise Topological Comparison with Merge Tree Neural Networks
Apr 08, 2024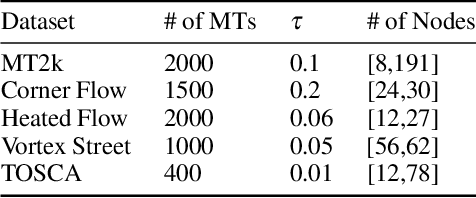
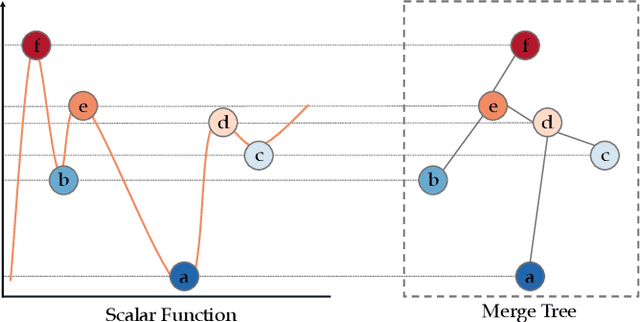
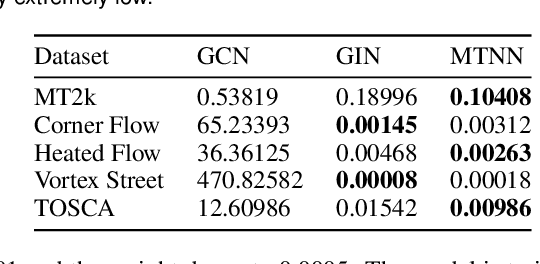
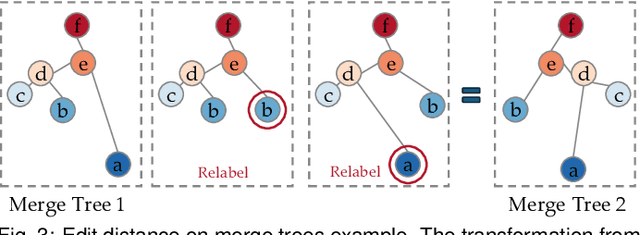
Abstract:Merge trees are a valuable tool in scientific visualization of scalar fields; however, current methods for merge tree comparisons are computationally expensive, primarily due to the exhaustive matching between tree nodes. To address this challenge, we introduce the merge tree neural networks (MTNN), a learned neural network model designed for merge tree comparison. The MTNN enables rapid and high-quality similarity computation. We first demonstrate how graph neural networks (GNNs), which emerged as an effective encoder for graphs, can be trained to produce embeddings of merge trees in vector spaces that enable efficient similarity comparison. Next, we formulate the novel MTNN model that further improves the similarity comparisons by integrating the tree and node embeddings with a new topological attention mechanism. We demonstrate the effectiveness of our model on real-world data in different domains and examine our model's generalizability across various datasets. Our experimental analysis demonstrates our approach's superiority in accuracy and efficiency. In particular, we speed up the prior state-of-the-art by more than 100x on the benchmark datasets while maintaining an error rate below 0.1%.
The Manifold Density Function: An Intrinsic Method for the Validation of Manifold Learning
Feb 14, 2024
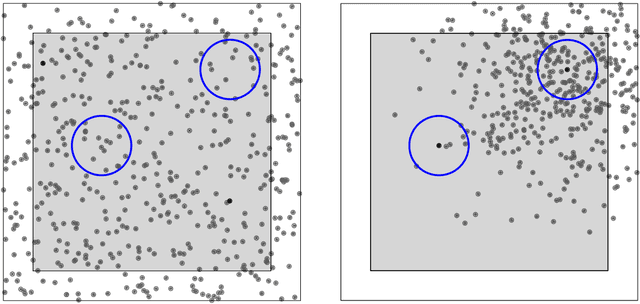

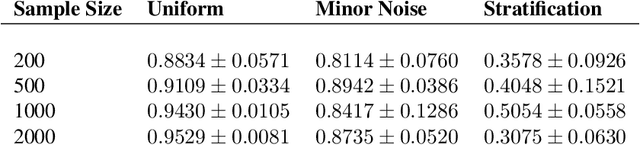
Abstract:We introduce the manifold density function, which is an intrinsic method to validate manifold learning techniques. Our approach adapts and extends Ripley's $K$-function, and categorizes in an unsupervised setting the extent to which an output of a manifold learning algorithm captures the structure of a latent manifold. Our manifold density function generalizes to broad classes of Riemannian manifolds. In particular, we extend the manifold density function to general two-manifolds using the Gauss-Bonnet theorem, and demonstrate that the manifold density function for hypersurfaces is well approximated using the first Laplacian eigenvalue. We prove desirable convergence and robustness properties.
Visualizing Topological Importance: A Class-Driven Approach
Sep 22, 2023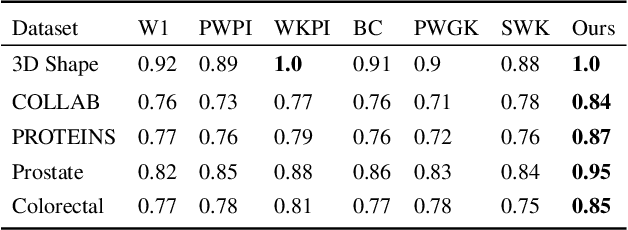
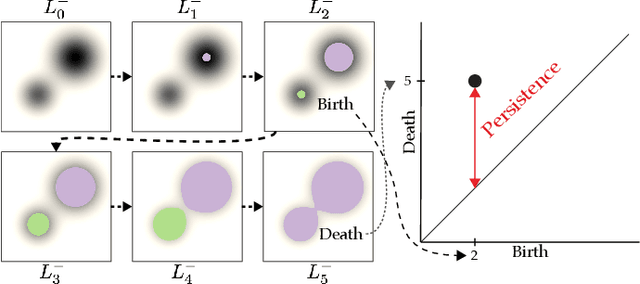
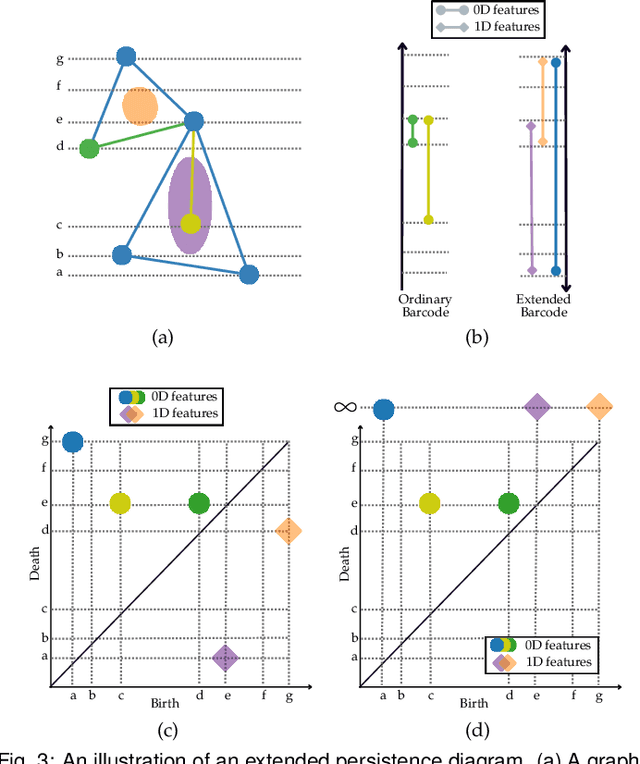
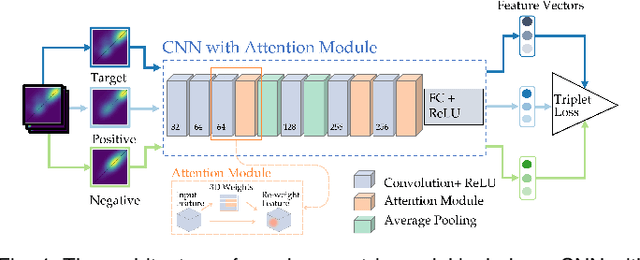
Abstract:This paper presents the first approach to visualize the importance of topological features that define classes of data. Topological features, with their ability to abstract the fundamental structure of complex data, are an integral component of visualization and analysis pipelines. Although not all topological features present in data are of equal importance. To date, the default definition of feature importance is often assumed and fixed. This work shows how proven explainable deep learning approaches can be adapted for use in topological classification. In doing so, it provides the first technique that illuminates what topological structures are important in each dataset in regards to their class label. In particular, the approach uses a learned metric classifier with a density estimator of the points of a persistence diagram as input. This metric learns how to reweigh this density such that classification accuracy is high. By extracting this weight, an importance field on persistent point density can be created. This provides an intuitive representation of persistence point importance that can be used to drive new visualizations. This work provides two examples: Visualization on each diagram directly and, in the case of sublevel set filtrations on images, directly on the images themselves. This work highlights real-world examples of this approach visualizing the important topological features in graph, 3D shape, and medical image data.
A Domain-Oblivious Approach for Learning Concise Representations of Filtered Topological Spaces
May 25, 2021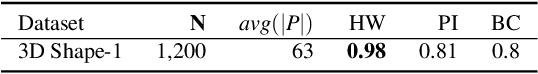
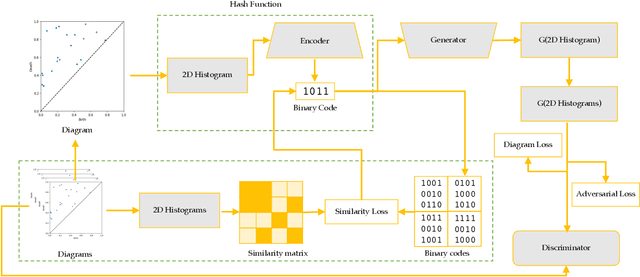

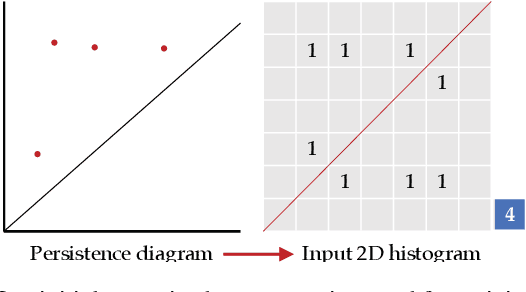
Abstract:Persistence diagrams have been widely used to quantify the underlying features of filtered topological spaces in data visualization. In many applications, computing distances between diagrams is essential; however, computing these distances has been challenging due to the computational cost. In this paper, we propose a persistence diagram hashing framework that learns a binary code representation of persistence diagrams, which allows for fast computation of distances. This framework is built upon a generative adversarial network (GAN) with a diagram distance loss function to steer the learning process. Instead of attempting to transform diagrams into vectorized representations, we hash diagrams into binary codes, which have natural advantages in large-scale tasks. The training of this model is domain-oblivious in that it can be computed purely from synthetic, randomly created diagrams. As a consequence, our proposed method is directly applicable to various datasets without the need of retraining the model. These binary codes, when compared using fast Hamming distance, better maintain topological similarity properties between datasets than other vectorized representations. To evaluate this method, we apply our framework to the problem of diagram clustering and we compare the quality and performance of our approach to the state-of-the-art. In addition, we show the scalability of our approach on a dataset with 10k persistence diagrams, which is not possible with current techniques. Moreover, our experimental results demonstrate that our method is significantly faster with less memory usage, while retaining comparable or better quality comparisons.
Confidence sets for persistence diagrams
Nov 20, 2014



Abstract:Persistent homology is a method for probing topological properties of point clouds and functions. The method involves tracking the birth and death of topological features (2000) as one varies a tuning parameter. Features with short lifetimes are informally considered to be "topological noise," and those with a long lifetime are considered to be "topological signal." In this paper, we bring some statistical ideas to persistent homology. In particular, we derive confidence sets that allow us to separate topological signal from topological noise.
* Published in at http://dx.doi.org/10.1214/14-AOS1252 the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge