On the Calibration of Epistemic Uncertainty: Principles, Paradoxes and Conflictual Loss

The calibration of predictive distributions has been widely studied in deep learning, but the same cannot be said about the more specific epistemic uncertainty as produced by Deep Ensembles, Bayesian Deep Networks, or Evidential Deep Networks. Although measurable, this form of uncertainty is difficult to calibrate on an objective basis as it depends on the prior for which a variety of choices exist. Nevertheless, epistemic uncertainty must in all cases satisfy two formal requirements: first, it must decrease when the training dataset gets larger and, second, it must increase when the model expressiveness grows. Despite these expectations, our experimental study shows that on several reference datasets and models, measures of epistemic uncertainty violate these requirements, sometimes presenting trends completely opposite to those expected. These paradoxes between expectation and reality raise the question of the true utility of epistemic uncertainty as estimated by these models. A formal argument suggests that this disagreement is due to a poor approximation of the posterior distribution rather than to a flaw in the measure itself. Based on this observation, we propose a regularization function for deep ensembles, called conflictual loss in line with the above requirements. We emphasize its strengths by showing experimentally that it restores both requirements of epistemic uncertainty, without sacrificing either the performance or the calibration of the deep ensembles.

Clarity: an improved gradient method for producing quality visual counterfactual explanations

Visual counterfactual explanations identify modifications to an image that would change the prediction of a classifier. We propose a set of techniques based on generative models (VAE) and a classifier ensemble directly trained in the latent space, which all together, improve the quality of the gradient required to compute visual counterfactuals. These improvements lead to a novel classification model, Clarity, which produces realistic counterfactual explanations over all images. We also present several experiments that give insights on why these techniques lead to better quality results than those in the literature. The explanations produced are competitive with the state-of-the-art and emphasize the importance of selecting a meaningful input space for training.

A Bayesian Convolutional Neural Network for Robust Galaxy Ellipticity Regression

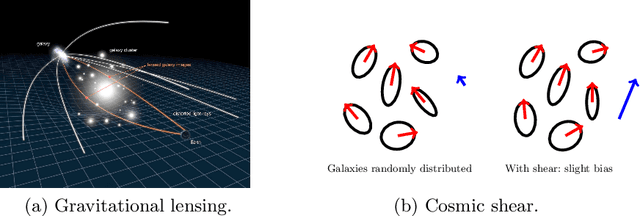
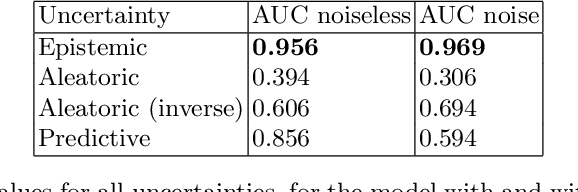
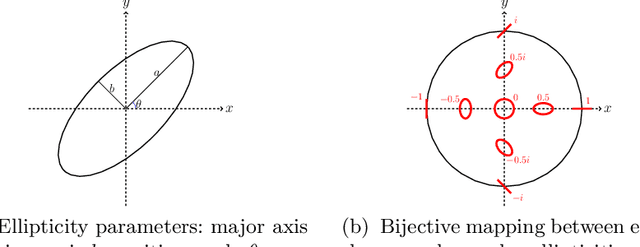
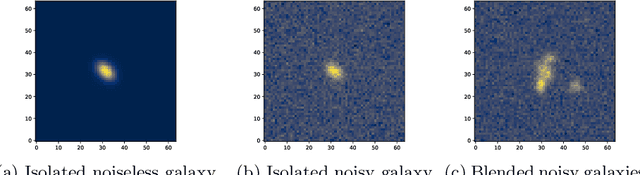
Cosmic shear estimation is an essential scientific goal for large galaxy surveys. It refers to the coherent distortion of distant galaxy images due to weak gravitational lensing along the line of sight. It can be used as a tracer of the matter distribution in the Universe. The unbiased estimation of the local value of the cosmic shear can be obtained via Bayesian analysis which relies on robust estimation of the galaxies ellipticity (shape) posterior distribution. This is not a simple problem as, among other things, the images may be corrupted with strong background noise. For current and coming surveys, another central issue in galaxy shape determination is the treatment of statistically dominant overlapping (blended) objects. We propose a Bayesian Convolutional Neural Network based on Monte-Carlo Dropout to reliably estimate the ellipticity of galaxies and the corresponding measurement uncertainties. We show that while a convolutional network can be trained to correctly estimate well calibrated aleatoric uncertainty, -- the uncertainty due to the presence of noise in the images -- it is unable to generate a trustworthy ellipticity distribution when exposed to previously unseen data (i.e. here, blended scenes). By introducing a Bayesian Neural Network, we show how to reliably estimate the posterior predictive distribution of ellipticities along with robust estimation of epistemic uncertainties. Experiments also show that epistemic uncertainty can detect inconsistent predictions due to unknown blended scenes.

A Bayesian Neural Network based on Dropout Regulation

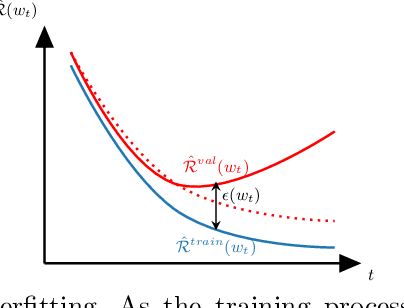
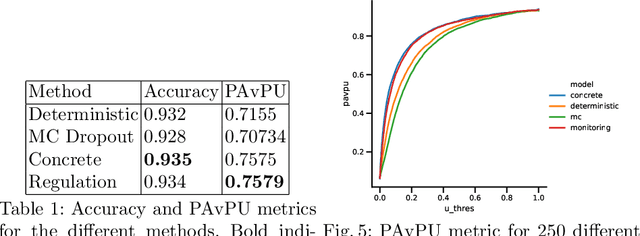
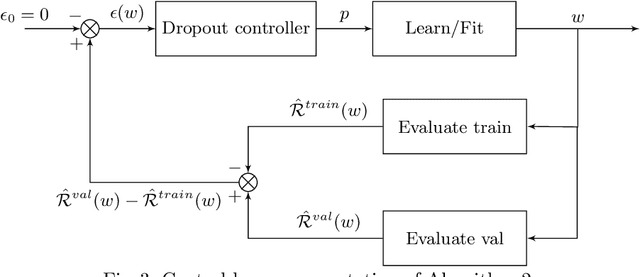
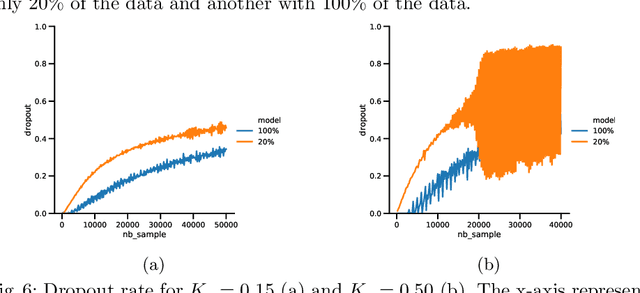
Bayesian Neural Networks (BNN) have recently emerged in the Deep Learning world for dealing with uncertainty estimation in classification tasks, and are used in many application domains such as astrophysics, autonomous driving...BNN assume a prior over the weights of a neural network instead of point estimates, enabling in this way the estimation of both aleatoric and epistemic uncertainty of the model prediction.Moreover, a particular type of BNN, namely MC Dropout, assumes a Bernoulli distribution on the weights by using Dropout.Several attempts to optimize the dropout rate exist, e.g. using a variational approach.In this paper, we present a new method called "Dropout Regulation" (DR), which consists of automatically adjusting the dropout rate during training using a controller as used in automation.DR allows for a precise estimation of the uncertainty which is comparable to the state-of-the-art while remaining simple to implement.

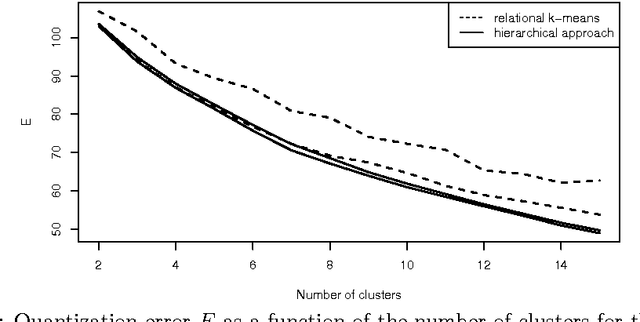
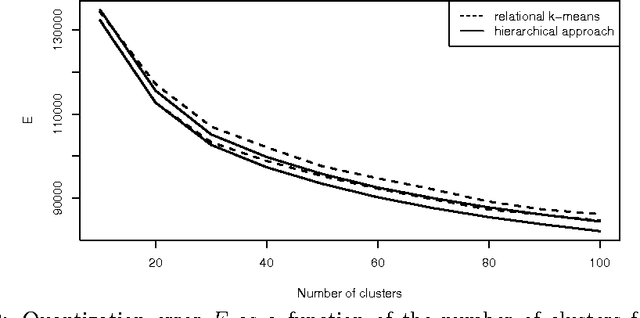
Dissimilarity Clustering by Hierarchical Multi-Level Refinement

We introduce in this paper a new way of optimizing the natural extension of the quantization error using in k-means clustering to dissimilarity data. The proposed method is based on hierarchical clustering analysis combined with multi-level heuristic refinement. The method is computationally efficient and achieves better quantization errors than the

Accélération des cartes auto-organisatrices sur tableau de dissimilarités par séparation et évaluation

In this paper, a new implementation of the adaptation of Kohonen self-organising maps (SOM) to dissimilarity matrices is proposed. This implementation relies on the branch and bound principle to reduce the algorithm running time. An important property of this new approach is that the obtained algorithm produces exactly the same results as the standard algorithm.

Multi-Layer Perceptrons and Symbolic Data

In some real world situations, linear models are not sufficient to represent accurately complex relations between input variables and output variables of a studied system. Multilayer Perceptrons are one of the most successful non-linear regression tool but they are unfortunately restricted to inputs and outputs that belong to a normed vector space. In this chapter, we propose a general recoding method that allows to use symbolic data both as inputs and outputs to Multilayer Perceptrons. The recoding is quite simple to implement and yet provides a flexible framework that allows to deal with almost all practical cases. The proposed method is illustrated on a real world data set.

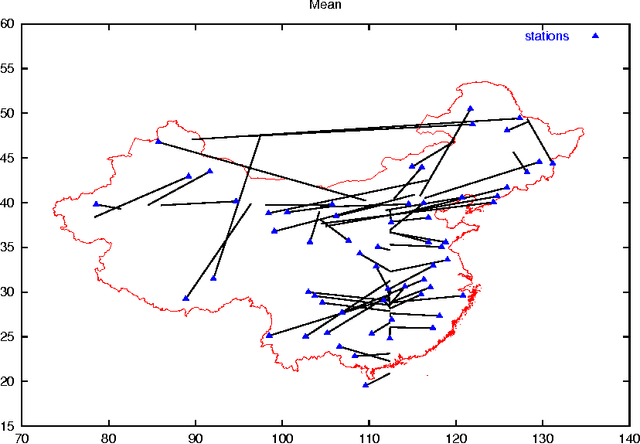
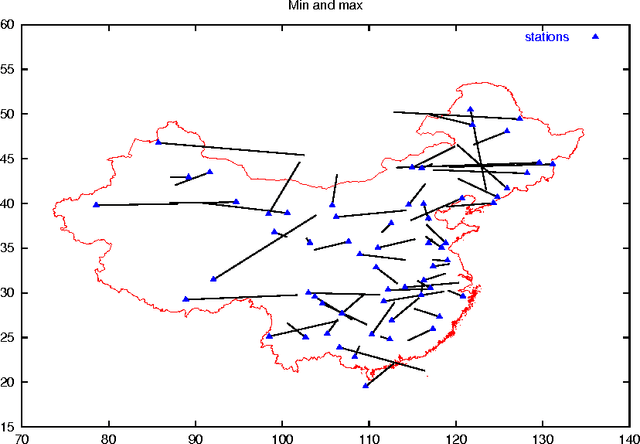
Functional Multi-Layer Perceptron: a Nonlinear Tool for Functional Data Analysis

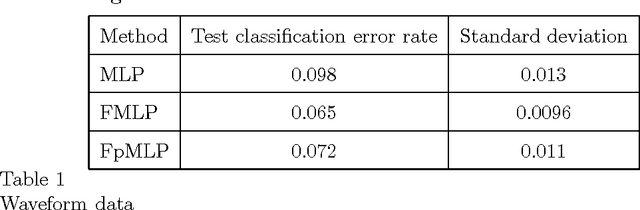
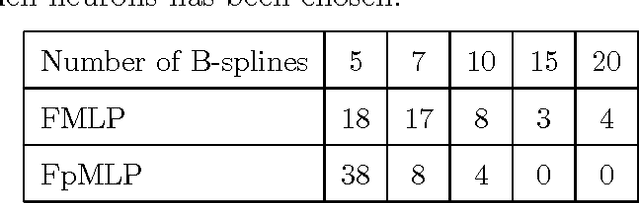
In this paper, we study a natural extension of Multi-Layer Perceptrons (MLP) to functional inputs. We show that fundamental results for classical MLP can be extended to functional MLP. We obtain universal approximation results that show the expressive power of functional MLP is comparable to that of numerical MLP. We obtain consistency results which imply that the estimation of optimal parameters for functional MLP is statistically well defined. We finally show on simulated and real world data that the proposed model performs in a very satisfactory way.

Representation of Functional Data in Neural Networks

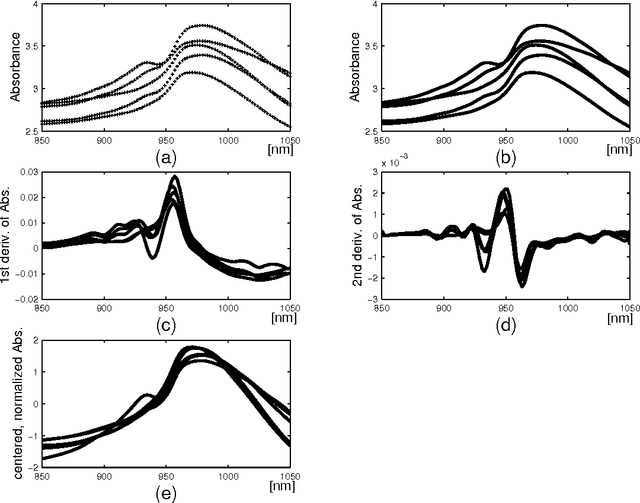
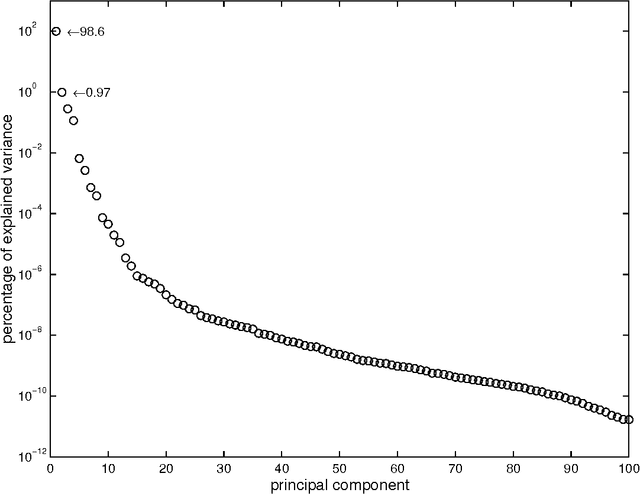
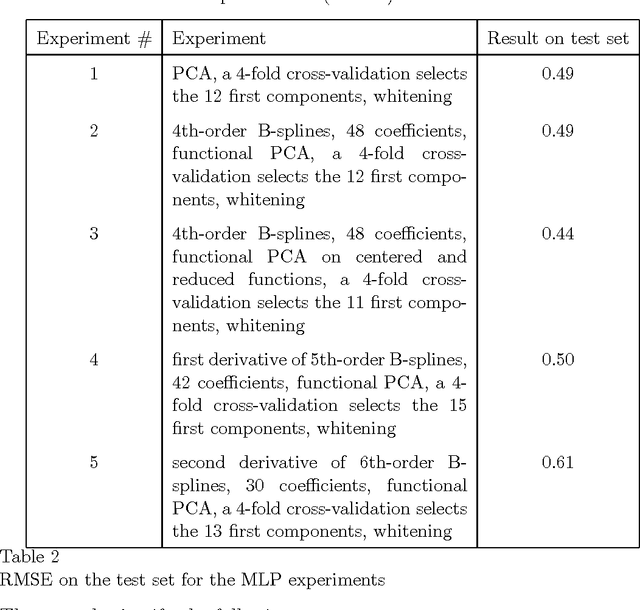
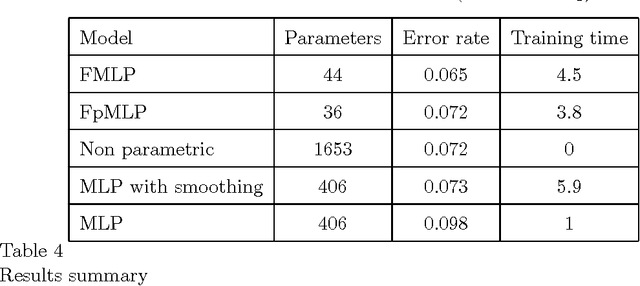
Functional Data Analysis (FDA) is an extension of traditional data analysis to functional data, for example spectra, temporal series, spatio-temporal images, gesture recognition data, etc. Functional data are rarely known in practice; usually a regular or irregular sampling is known. For this reason, some processing is needed in order to benefit from the smooth character of functional data in the analysis methods. This paper shows how to extend the Radial-Basis Function Networks (RBFN) and Multi-Layer Perceptron (MLP) models to functional data inputs, in particular when the latter are known through lists of input-output pairs. Various possibilities for functional processing are discussed, including the projection on smooth bases, Functional Principal Component Analysis, functional centering and reduction, and the use of differential operators. It is shown how to incorporate these functional processing into the RBFN and MLP models. The functional approach is illustrated on a benchmark of spectrometric data analysis.

Self-organizing maps and symbolic data

In data analysis new forms of complex data have to be considered like for example (symbolic data, functional data, web data, trees, SQL query and multimedia data, ...). In this context classical data analysis for knowledge discovery based on calculating the center of gravity can not be used because input are not $\mathbb{R}^p$ vectors. In this paper, we present an application on real world symbolic data using the self-organizing map. To this end, we propose an extension of the self-organizing map that can handle symbolic data.