A Bayesian Convolutional Neural Network for Robust Galaxy Ellipticity Regression

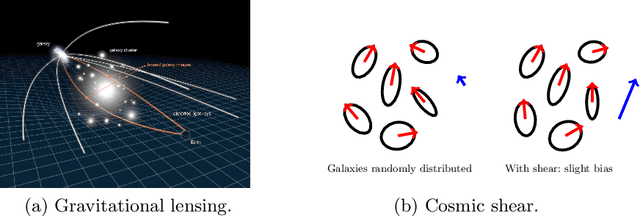
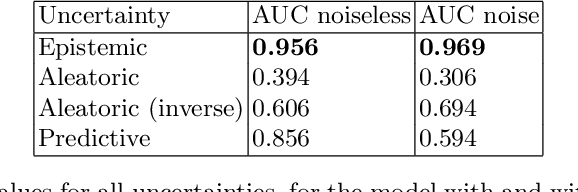
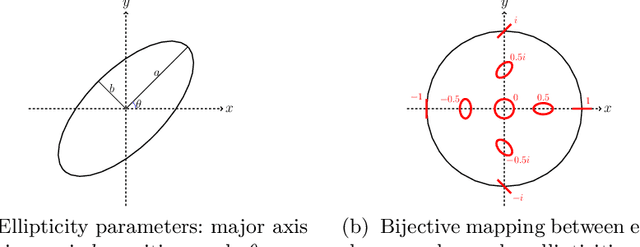
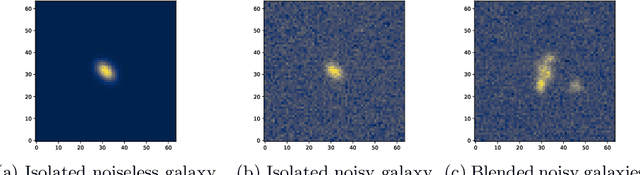
Cosmic shear estimation is an essential scientific goal for large galaxy surveys. It refers to the coherent distortion of distant galaxy images due to weak gravitational lensing along the line of sight. It can be used as a tracer of the matter distribution in the Universe. The unbiased estimation of the local value of the cosmic shear can be obtained via Bayesian analysis which relies on robust estimation of the galaxies ellipticity (shape) posterior distribution. This is not a simple problem as, among other things, the images may be corrupted with strong background noise. For current and coming surveys, another central issue in galaxy shape determination is the treatment of statistically dominant overlapping (blended) objects. We propose a Bayesian Convolutional Neural Network based on Monte-Carlo Dropout to reliably estimate the ellipticity of galaxies and the corresponding measurement uncertainties. We show that while a convolutional network can be trained to correctly estimate well calibrated aleatoric uncertainty, -- the uncertainty due to the presence of noise in the images -- it is unable to generate a trustworthy ellipticity distribution when exposed to previously unseen data (i.e. here, blended scenes). By introducing a Bayesian Neural Network, we show how to reliably estimate the posterior predictive distribution of ellipticities along with robust estimation of epistemic uncertainties. Experiments also show that epistemic uncertainty can detect inconsistent predictions due to unknown blended scenes.