On the Calibration of Epistemic Uncertainty: Principles, Paradoxes and Conflictual Loss

The calibration of predictive distributions has been widely studied in deep learning, but the same cannot be said about the more specific epistemic uncertainty as produced by Deep Ensembles, Bayesian Deep Networks, or Evidential Deep Networks. Although measurable, this form of uncertainty is difficult to calibrate on an objective basis as it depends on the prior for which a variety of choices exist. Nevertheless, epistemic uncertainty must in all cases satisfy two formal requirements: first, it must decrease when the training dataset gets larger and, second, it must increase when the model expressiveness grows. Despite these expectations, our experimental study shows that on several reference datasets and models, measures of epistemic uncertainty violate these requirements, sometimes presenting trends completely opposite to those expected. These paradoxes between expectation and reality raise the question of the true utility of epistemic uncertainty as estimated by these models. A formal argument suggests that this disagreement is due to a poor approximation of the posterior distribution rather than to a flaw in the measure itself. Based on this observation, we propose a regularization function for deep ensembles, called conflictual loss in line with the above requirements. We emphasize its strengths by showing experimentally that it restores both requirements of epistemic uncertainty, without sacrificing either the performance or the calibration of the deep ensembles.

The Epistemic Uncertainty Hole: an issue of Bayesian Neural Networks

Bayesian Deep Learning (BDL) gives access not only to aleatoric uncertainty, as standard neural networks already do, but also to epistemic uncertainty, a measure of confidence a model has in its own predictions. In this article, we show through experiments that the evolution of epistemic uncertainty metrics regarding the model size and the size of the training set, goes against theoretical expectations. More precisely, we observe that the epistemic uncertainty collapses literally in the presence of large models and sometimes also of little training data, while we expect the exact opposite behaviour. This phenomenon, which we call "epistemic uncertainty hole", is all the more problematic as it undermines the entire applicative potential of BDL, which is based precisely on the use of epistemic uncertainty. As an example, we evaluate the practical consequences of this uncertainty hole on one of the main applications of BDL, namely the detection of out-of-distribution samples

Clarity: an improved gradient method for producing quality visual counterfactual explanations

Visual counterfactual explanations identify modifications to an image that would change the prediction of a classifier. We propose a set of techniques based on generative models (VAE) and a classifier ensemble directly trained in the latent space, which all together, improve the quality of the gradient required to compute visual counterfactuals. These improvements lead to a novel classification model, Clarity, which produces realistic counterfactual explanations over all images. We also present several experiments that give insights on why these techniques lead to better quality results than those in the literature. The explanations produced are competitive with the state-of-the-art and emphasize the importance of selecting a meaningful input space for training.

A Bayesian Convolutional Neural Network for Robust Galaxy Ellipticity Regression

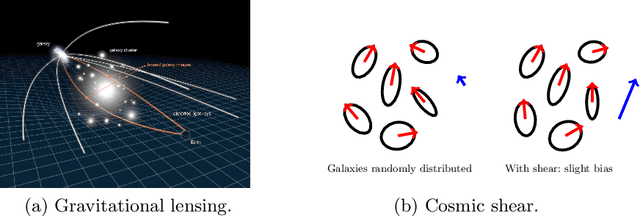
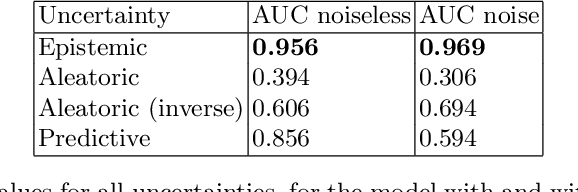
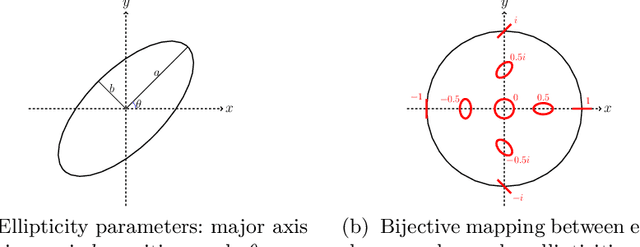
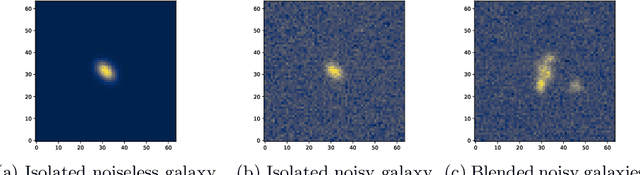
Cosmic shear estimation is an essential scientific goal for large galaxy surveys. It refers to the coherent distortion of distant galaxy images due to weak gravitational lensing along the line of sight. It can be used as a tracer of the matter distribution in the Universe. The unbiased estimation of the local value of the cosmic shear can be obtained via Bayesian analysis which relies on robust estimation of the galaxies ellipticity (shape) posterior distribution. This is not a simple problem as, among other things, the images may be corrupted with strong background noise. For current and coming surveys, another central issue in galaxy shape determination is the treatment of statistically dominant overlapping (blended) objects. We propose a Bayesian Convolutional Neural Network based on Monte-Carlo Dropout to reliably estimate the ellipticity of galaxies and the corresponding measurement uncertainties. We show that while a convolutional network can be trained to correctly estimate well calibrated aleatoric uncertainty, -- the uncertainty due to the presence of noise in the images -- it is unable to generate a trustworthy ellipticity distribution when exposed to previously unseen data (i.e. here, blended scenes). By introducing a Bayesian Neural Network, we show how to reliably estimate the posterior predictive distribution of ellipticities along with robust estimation of epistemic uncertainties. Experiments also show that epistemic uncertainty can detect inconsistent predictions due to unknown blended scenes.

A Bayesian Neural Network based on Dropout Regulation

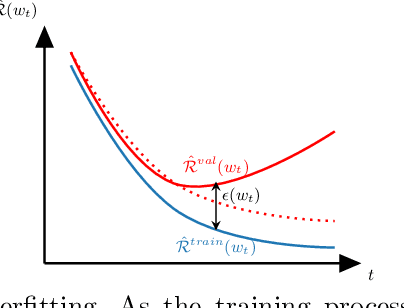
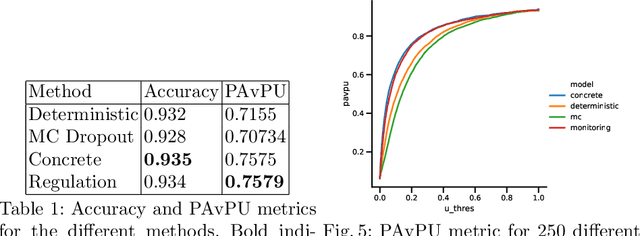
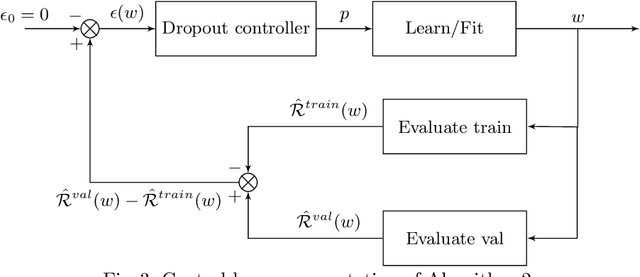
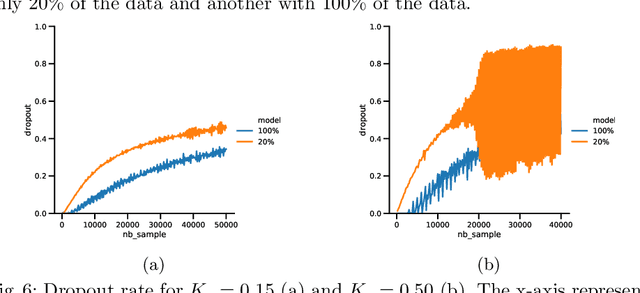
Bayesian Neural Networks (BNN) have recently emerged in the Deep Learning world for dealing with uncertainty estimation in classification tasks, and are used in many application domains such as astrophysics, autonomous driving...BNN assume a prior over the weights of a neural network instead of point estimates, enabling in this way the estimation of both aleatoric and epistemic uncertainty of the model prediction.Moreover, a particular type of BNN, namely MC Dropout, assumes a Bernoulli distribution on the weights by using Dropout.Several attempts to optimize the dropout rate exist, e.g. using a variational approach.In this paper, we present a new method called "Dropout Regulation" (DR), which consists of automatically adjusting the dropout rate during training using a controller as used in automation.DR allows for a precise estimation of the uncertainty which is comparable to the state-of-the-art while remaining simple to implement.