Self-organizing maps and symbolic data

In data analysis new forms of complex data have to be considered like for example (symbolic data, functional data, web data, trees, SQL query and multimedia data, ...). In this context classical data analysis for knowledge discovery based on calculating the center of gravity can not be used because input are not $\mathbb{R}^p$ vectors. In this paper, we present an application on real world symbolic data using the self-organizing map. To this end, we propose an extension of the self-organizing map that can handle symbolic data.

Une adaptation des cartes auto-organisatrices pour des données décrites par un tableau de dissimilarités

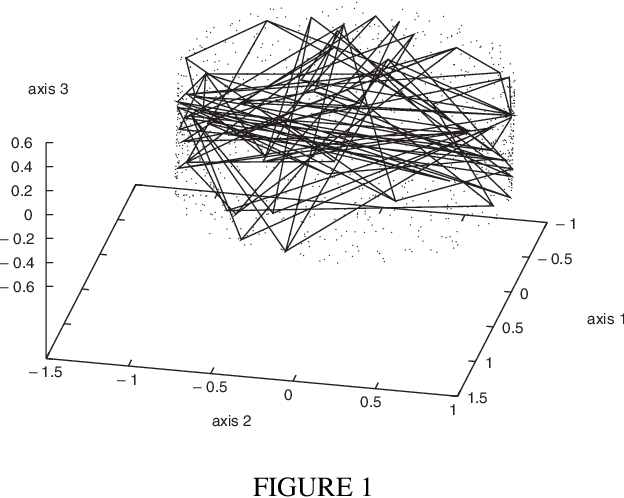
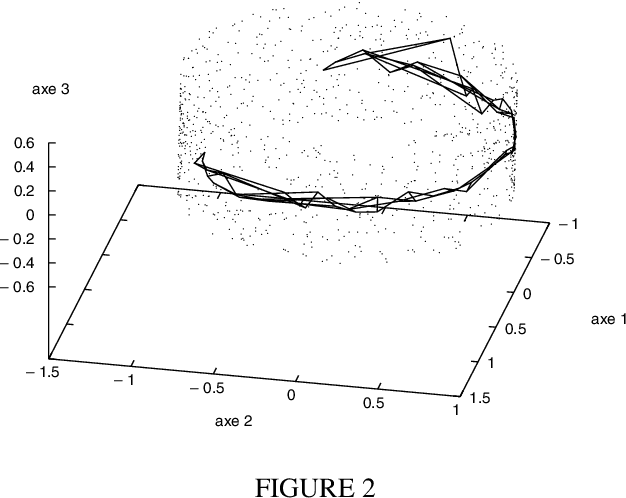
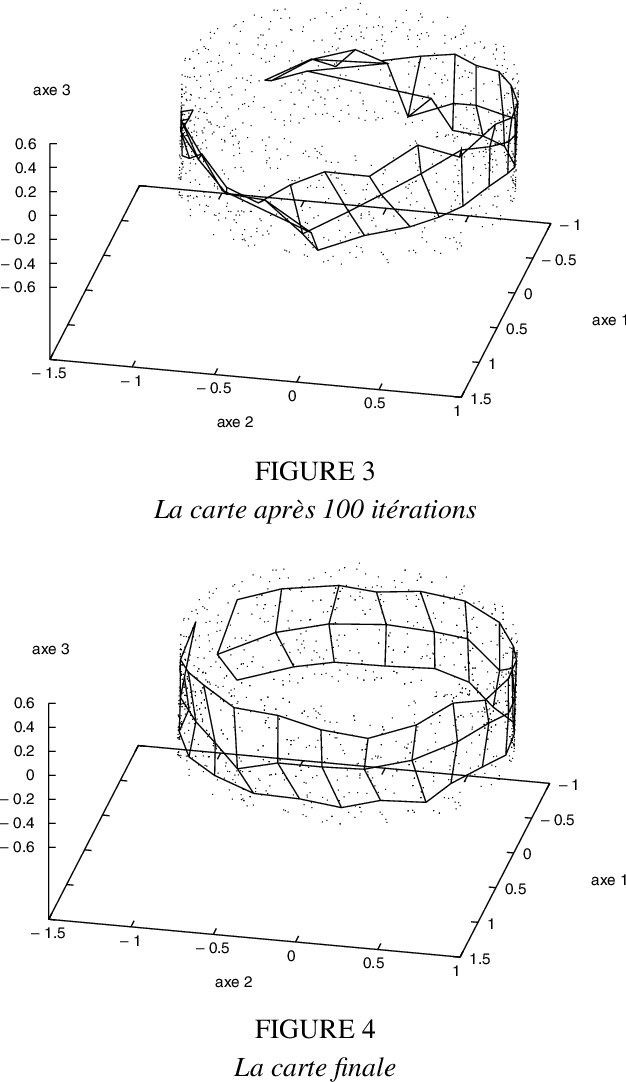
Many data analysis methods cannot be applied to data that are not represented by a fixed number of real values, whereas most of real world observations are not readily available in such a format. Vector based data analysis methods have therefore to be adapted in order to be used with non standard complex data. A flexible and general solution for this adaptation is to use a (dis)similarity measure. Indeed, thanks to expert knowledge on the studied data, it is generally possible to define a measure that can be used to make pairwise comparison between observations. General data analysis methods are then obtained by adapting existing methods to (dis)similarity matrices. In this article, we propose an adaptation of Kohonen's Self Organizing Map (SOM) to (dis)similarity data. The proposed algorithm is an adapted version of the vector based batch SOM. The method is validated on real world data: we provide an analysis of the usage patterns of the web site of the Institut National de Recherche en Informatique et Automatique, constructed thanks to web log mining method.

Fast Algorithm and Implementation of Dissimilarity Self-Organizing Maps

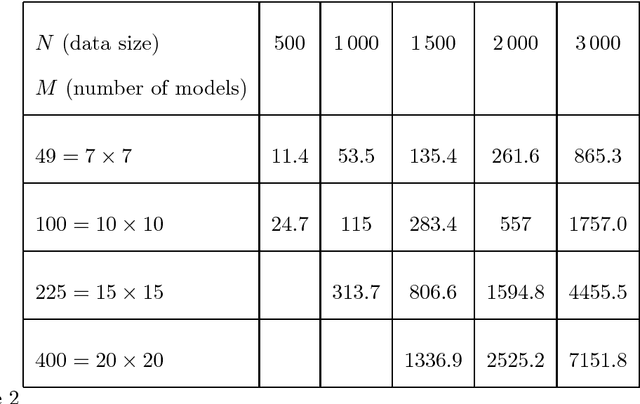
In many real world applications, data cannot be accurately represented by vectors. In those situations, one possible solution is to rely on dissimilarity measures that enable sensible comparison between observations. Kohonen's Self-Organizing Map (SOM) has been adapted to data described only through their dissimilarity matrix. This algorithm provides both non linear projection and clustering of non vector data. Unfortunately, the algorithm suffers from a high cost that makes it quite difficult to use with voluminous data sets. In this paper, we propose a new algorithm that provides an important reduction of the theoretical cost of the dissimilarity SOM without changing its outcome (the results are exactly the same as the ones obtained with the original algorithm). Moreover, we introduce implementation methods that result in very short running times. Improvements deduced from the theoretical cost model are validated on simulated and real world data (a word list clustering problem). We also demonstrate that the proposed implementation methods reduce by a factor up to 3 the running time of the fast algorithm over a standard implementation.