When Tables Leak: Attacking String Memorization in LLM-Based Tabular Data Generation

Large Language Models (LLMs) have recently demonstrated remarkable performance in generating high-quality tabular synthetic data. In practice, two primary approaches have emerged for adapting LLMs to tabular data generation: (i) fine-tuning smaller models directly on tabular datasets, and (ii) prompting larger models with examples provided in context. In this work, we show that popular implementations from both regimes exhibit a tendency to compromise privacy by reproducing memorized patterns of numeric digits from their training data. To systematically analyze this risk, we introduce a simple No-box Membership Inference Attack (MIA) called LevAtt that assumes adversarial access to only the generated synthetic data and targets the string sequences of numeric digits in synthetic observations. Using this approach, our attack exposes substantial privacy leakage across a wide range of models and datasets, and in some cases, is even a perfect membership classifier on state-of-the-art models. Our findings highlight a unique privacy vulnerability of LLM-based synthetic data generation and the need for effective defenses. To this end, we propose two methods, including a novel sampling strategy that strategically perturbs digits during generation. Our evaluation demonstrates that this approach can defeat these attacks with minimal loss of fidelity and utility of the synthetic data.

Watermarking Generative Categorical Data

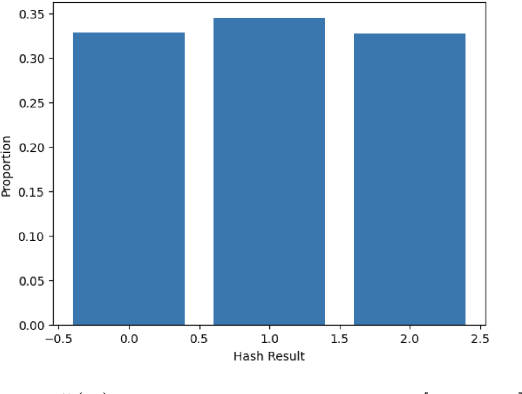
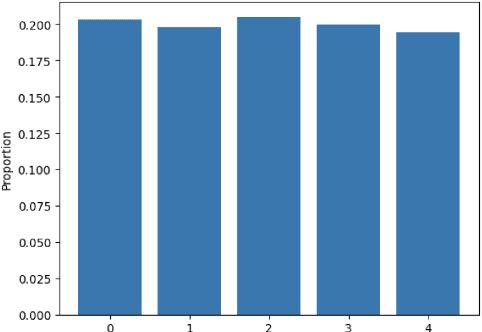
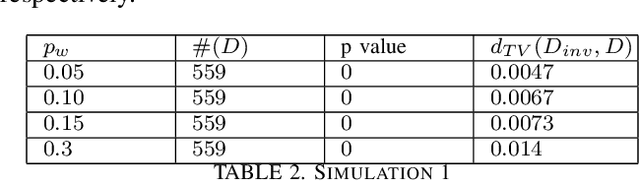
In this paper, we propose a novel statistical framework for watermarking generative categorical data. Our method systematically embeds pre-agreed secret signals by splitting the data distribution into two components and modifying one distribution based on a deterministic relationship with the other, ensuring the watermark is embedded at the distribution-level. To verify the watermark, we introduce an insertion inverse algorithm and detect its presence by measuring the total variation distance between the inverse-decoded data and the original distribution. Unlike previous categorical watermarking methods, which primarily focus on embedding watermarks into a given dataset, our approach operates at the distribution-level, allowing for verification from a statistical distributional perspective. This makes it particularly well-suited for the modern paradigm of synthetic data generation, where the underlying data distribution, rather than specific data points, is of primary importance. The effectiveness of our method is demonstrated through both theoretical analysis and empirical validation.

Under-Parameterized Double Descent for Ridge Regularized Least Squares Denoising of Data on a Line

The relationship between the number of training data points, the number of parameters in a statistical model, and the generalization capabilities of the model has been widely studied. Previous work has shown that double descent can occur in the over-parameterized regime, and believe that the standard bias-variance trade-off holds in the under-parameterized regime. In this paper, we present a simple example that provably exhibits double descent in the under-parameterized regime. For simplicity, we look at the ridge regularized least squares denoising problem with data on a line embedded in high-dimension space. By deriving an asymptotically accurate formula for the generalization error, we observe sample-wise and parameter-wise double descent with the peak in the under-parameterized regime rather than at the interpolation point or in the over-parameterized regime. Further, the peak of the sample-wise double descent curve corresponds to a peak in the curve for the norm of the estimator, and adjusting $\mu$, the strength of the ridge regularization, shifts the location of the peak. We observe that parameter-wise double descent occurs for this model for small $\mu$. For larger values of $\mu$, we observe that the curve for the norm of the estimator has a peak but that this no longer translates to a peak in the generalization error. Moreover, we study the training error for this problem. The considered problem setup allows for studying the interaction between two regularizers. We provide empirical evidence that the model implicitly favors using the ridge regularizer over the input data noise regularizer. Thus, we show that even though both regularizers regularize the same quantity, i.e., the norm of the estimator, they are not equivalent.