Learning Hybrid Policies for MPC with Application to Drone Flight in Unknown Dynamic Environments

In recent years, drones have found increased applications in a wide array of real-world tasks. Model predictive control (MPC) has emerged as a practical method for drone flight control, owing to its robustness against modeling errors/uncertainties and external disturbances. However, MPC's sensitivity to manually tuned parameters can lead to rapid performance degradation when faced with unknown environmental dynamics. This paper addresses the challenge of controlling a drone as it traverses a swinging gate characterized by unknown dynamics. This paper introduces a parameterized MPC approach named hyMPC that leverages high-level decision variables to adapt to uncertain environmental conditions. To derive these decision variables, a novel policy search framework aimed at training a high-level Gaussian policy is presented. Subsequently, we harness the power of neural network policies, trained on data gathered through the repeated execution of the Gaussian policy, to provide real-time decision variables. The effectiveness of hyMPC is validated through numerical simulations, achieving a 100\% success rate in 20 drone flight tests traversing a swinging gate, demonstrating its capability to achieve safe and precise flight with limited prior knowledge of environmental dynamics.

A Hybrid Decomposition-based Multi-objective Evolutionary Algorithm for the Multi-Point Dynamic Aggregation Problem

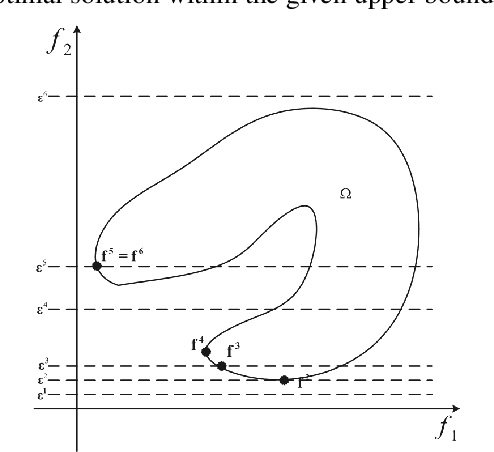
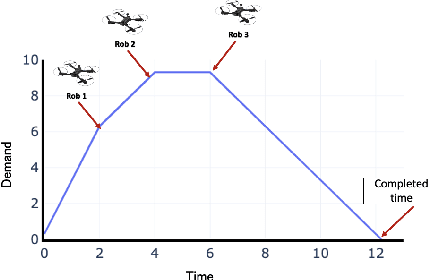
An emerging optimisation problem from the real-world applications, named the multi-point dynamic aggregation (MPDA) problem, has become one of the active research topics of the multi-robot system. This paper focuses on a multi-objective MPDA problem which is to design an execution plan of the robots to minimise the number of robots and the maximal completion time of all the tasks. The strongly-coupled relationships among robots and tasks, the redundancy of the MPDA encoding, and the variable-size decision space of the MO-MPDA problem posed extra challenges for addressing the problem effectively. To address the above issues, we develop a hybrid decomposition-based multi-objective evolutionary algorithm (HDMOEA) using $ \varepsilon $-constraint method. It selects the maximal completion time of all tasks as the main objective, and converted the other objective into constraints. HDMOEA decomposes a MO-MPDA problem into a series of scalar constrained optimization subproblems by assigning each subproblem with an upper bound robot number. All the subproblems are optimized simultaneously with the transferring knowledge from other subproblems. Besides, we develop a hybrid population initialisation mechanism to enhance the quality of initial solutions, and a reproduction mechanism to transmit effective information and tackle the encoding redundancy. Experimental results show that the proposed HDMOEA method significantly outperforms the state-of-the-art methods in terms of several most-used metrics.