C$^3$DG: Conditional Domain Generalization for Hyperspectral Imagery Classification with Convergence and Constrained-risk Theories

Hyperspectral imagery (HSI) classification may suffer the challenge of hyperspectral-monospectra, where different classes present similar spectra. Joint spatial-spectral feature extraction is a popular solution for the problem, but this strategy tends to inflate accuracy since test pixels may exist in training patches. Domain generalization methods show promising potential, but they still fail to distinguish similar spectra across varying domains, in addition, the theoretical support is usually ignored. In this paper, we only rely on spectral information to solve the hyperspectral-monospectra problem, and propose a Convergence and Error-Constrained Conditional Domain Generalization method for Hyperspectral Imagery Classification (C$^3$DG). The major contributions of this paper include two aspects: the Conditional Revising Inference Block (CRIB), and the corresponding theories for model convergence and generalization errors. CRIB is the kernel structure of the proposed method, which employs a shared encoder and multi-branch decoders to fully leverage the conditional distribution during training, achieving a decoupling that aligns with the generation mechanisms of HSI. Moreover, to ensure model convergence and maintain controllable error, we propose the optimization convergence theorem and risk upper bound theorem. In the optimization convergence theorem, we ensure the model convergence by demonstrating that the gradients of the loss terms are not contradictory. In the risk upper bound theorem, our theoretical analysis explores the relationship between test-time training and recent related work to establish a concrete bound for error. Experimental results on three benchmark datasets indicate the superiority of C$^3$DG.

Domain Agnostic Conditional Invariant Predictions for Domain Generalization

Domain generalization aims to develop a model that can perform well on unseen target domains by learning from multiple source domains. However, recent-proposed domain generalization models usually rely on domain labels, which may not be available in many real-world scenarios. To address this challenge, we propose a Discriminant Risk Minimization (DRM) theory and the corresponding algorithm to capture the invariant features without domain labels. In DRM theory, we prove that reducing the discrepancy of prediction distribution between overall source domain and any subset of it can contribute to obtaining invariant features. To apply the DRM theory, we develop an algorithm which is composed of Bayesian inference and a new penalty termed as Categorical Discriminant Risk (CDR). In Bayesian inference, we transform the output of the model into a probability distribution to align with our theoretical assumptions. We adopt sliding update approach to approximate the overall prediction distribution of the model, which enables us to obtain CDR penalty. We also indicate the effectiveness of these components in finding invariant features. We evaluate our algorithm against various domain generalization methods on multiple real-world datasets, providing empirical support for our theory.

Domain Generalization Guided by Large-Scale Pre-Trained Priors

Domain generalization (DG) aims to train a model from limited source domains, allowing it to generalize to unknown target domains. Typically, DG models only employ large-scale pre-trained models during the initialization of fine-tuning. However, large-scale pre-trained models already possess the ability to resist domain shift. If we reference pre-trained models continuously during fine-tuning to maintain this ability, it could further enhance the generalization ability of the DG model. For this purpose, we introduce a new method called Fine-Tune with Large-scale pre-trained Priors (FT-LP), which incorporates the pre-trained model as a prior into the DG fine-tuning process, ensuring that the model refers to its pre-trained model at each optimization step. FT-LP comprises a theoretical framework and a simple implementation strategy. In theory, we verify the rationality of FT-LP by introducing a generalization error bound with the pre-trained priors for DG. In implementation, we utilize an encoder to simulate the model distribution, enabling the use of FT-LP when only pre-trained weights are available. In summary, we offer a new fine-tuning method for DG algorithms to utilize pre-trained models throughout the fine-tuning process. Through experiments on various datasets and DG models, our proposed method exhibits significant improvements, indicating its effectiveness.

Bayesian Domain Invariant Learning via Posterior Generalization of Parameter Distributions

Domain invariant learning aims to learn models that extract invariant features over various training domains, resulting in better generalization to unseen target domains. Recently, Bayesian Neural Networks have achieved promising results in domain invariant learning, but most works concentrate on aligning features distributions rather than parameter distributions. Inspired by the principle of Bayesian Neural Network, we attempt to directly learn the domain invariant posterior distribution of network parameters. We first propose a theorem to show that the invariant posterior of parameters can be implicitly inferred by aggregating posteriors on different training domains. Our assumption is more relaxed and allows us to extract more domain invariant information. We also propose a simple yet effective method, named PosTerior Generalization (PTG), that can be used to estimate the invariant parameter distribution. PTG fully exploits variational inference to approximate parameter distributions, including the invariant posterior and the posteriors on training domains. Furthermore, we develop a lite version of PTG for widespread applications. PTG shows competitive performance on various domain generalization benchmarks on DomainBed. Additionally, PTG can use any existing domain generalization methods as its prior, and combined with previous state-of-the-art method the performance can be further improved. Code will be made public.

Be Bayesian by Attachments to Catch More Uncertainty

Bayesian Neural Networks (BNNs) have become one of the promising approaches for uncertainty estimation due to the solid theorical foundations. However, the performance of BNNs is affected by the ability of catching uncertainty. Instead of only seeking the distribution of neural network weights by in-distribution (ID) data, in this paper, we propose a new Bayesian Neural Network with an Attached structure (ABNN) to catch more uncertainty from out-of-distribution (OOD) data. We first construct a mathematical description for the uncertainty of OOD data according to the prior distribution, and then develop an attached Bayesian structure to integrate the uncertainty of OOD data into the backbone network. ABNN is composed of an expectation module and several distribution modules. The expectation module is a backbone deep network which focuses on the original task, and the distribution modules are mini Bayesian structures which serve as attachments of the backbone. In particular, the distribution modules aim at extracting the uncertainty from both ID and OOD data. We further provide theoretical analysis for the convergence of ABNN, and experimentally validate its superiority by comparing with some state-of-the-art uncertainty estimation methods Code will be made available.

Spatial-Spectral Feedback Network for Super-Resolution of Hyperspectral Imagery

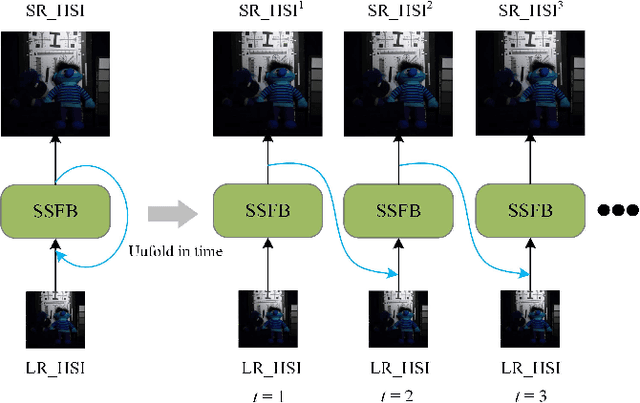
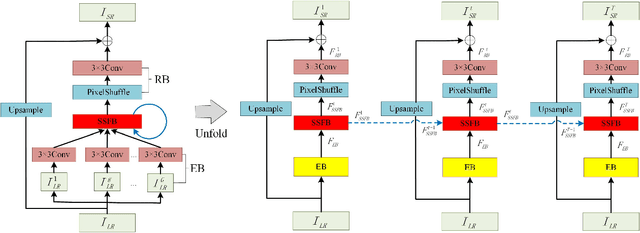
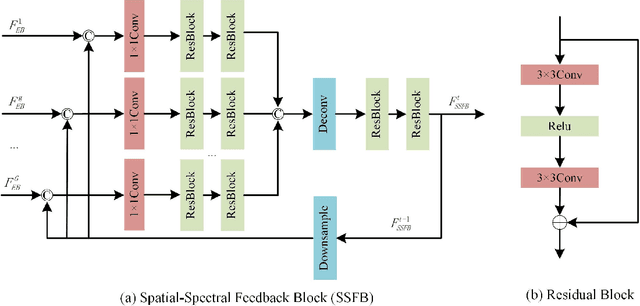
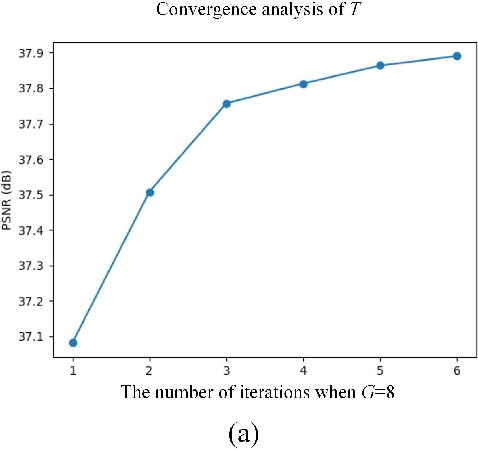
Recently, single gray/RGB image super-resolution (SR) methods based on deep learning have achieved great success. However, there are two obstacles to limit technical development in the single hyperspectral image super-resolution. One is the high-dimensional and complex spectral patterns in hyperspectral image, which make it difficult to explore spatial information and spectral information among bands simultaneously. The other is that the number of available hyperspectral training samples is extremely small, which can easily lead to overfitting when training a deep neural network. To address these issues, in this paper, we propose a novel Spatial-Spectral Feedback Network (SSFN) to refine low-level representations among local spectral bands with high-level information from global spectral bands. It will not only alleviate the difficulty in feature extraction due to high dimensional of hyperspectral data, but also make the training process more stable. Specifically, we use hidden states in an RNN with finite unfoldings to achieve such feedback manner. To exploit the spatial and spectral prior, a Spatial-Spectral Feedback Block (SSFB) is designed to handle the feedback connections and generate powerful high-level representations. The proposed SSFN comes with a early predictions and can reconstruct the final high-resolution hyperspectral image step by step. Extensive experimental results on three benchmark datasets demonstrate that the proposed SSFN achieves superior performance in comparison with the state-of-the-art methods. The source code is available at https://github.com/tangzhenjie/SSFN.

SRDA-Net: Super-Resolution Domain Adaptation Networks for Semantic Segmentation

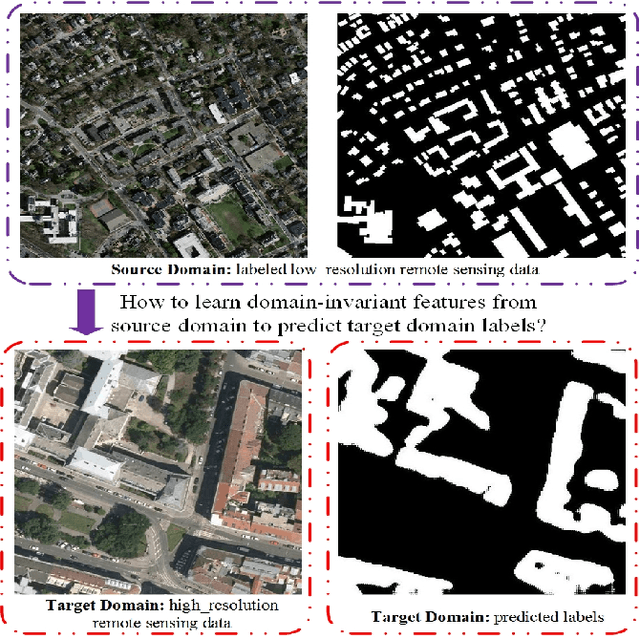
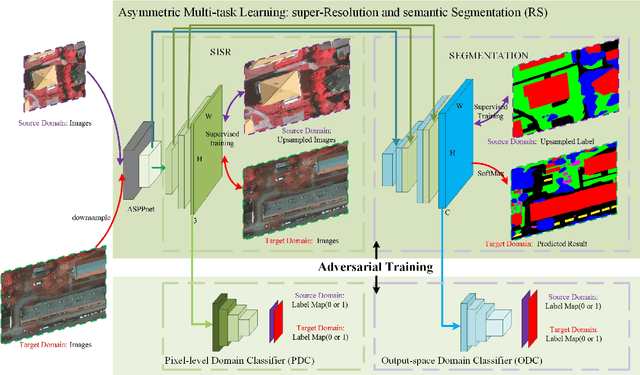
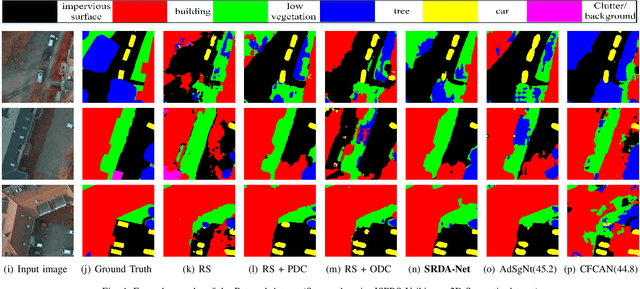
Recently, Unsupervised Domain Adaptation was proposed to address the domain shift problem in semantic segmentation task, but it may perform poor when source and target domains belong to different resolutions. In this work, we design a novel end-to-end semantic segmentation network, Super-Resolution Domain Adaptation Network (SRDA-Net), which could simultaneously complete super-resolution and domain adaptation. Such characteristics exactly meet the requirement of semantic segmentation for remote sensing images which usually involve various resolutions. Generally, SRDA-Net includes three deep neural networks: a Super-Resolution and Segmentation (SRS) model focuses on recovering high-resolution image and predicting segmentation map; a pixel-level domain classifier (PDC) tries to distinguish the images from which domains; and output-space domain classifier (ODC) discriminates pixel label distributions from which domains. PDC and ODC are considered as the discriminators, and SRS is treated as the generator. By the adversarial learning, SRS tries to align the source with target domains on pixel-level visual appearance and output-space. Experiments are conducted on the two remote sensing datasets with different resolutions. SRDA-Net performs favorably against the state-of-the-art methods in terms of accuracy and visual quality. Code and models are available at https://github.com/tangzhenjie/SRDA-Net.