Delay-Doppler Signal Processing with Zadoff-Chu Sequences

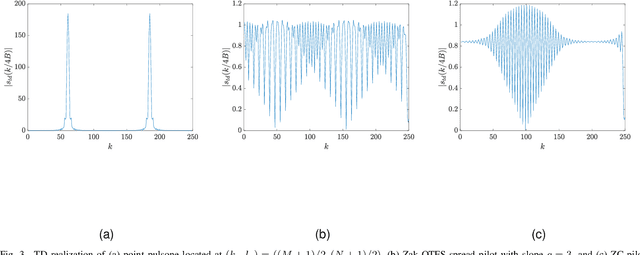
Much of the engineering behind current wireless systems has focused on designing an efficient and high-throughput downlink to support human-centric communication such as video streaming and internet browsing. This paper looks ahead to design of the uplink, anticipating the emergence of machine-type communication (MTC) and the confluence of sensing, communication, and distributed learning. We demonstrate that grant-free multiple access is possible even in the presence of highly time-varying channels. Our approach provides a pathway to standards adoption, since it is built on enhancing the 2-step random access procedure which is already part of the 5GNR standard. This 2-step procedure uses Zadoff-Chu (ZC) sequences as preambles that point to radio resources which are then used to upload data. We also use ZC sequences as preambles / pilots, but we process signals in the Delay-Doppler (DD) domain rather than the time-domain. We demonstrate that it is possible to detect multiple preambles in the presence of mobility and delay spread using a receiver with no knowledge of the channel other than the worst case delay and Doppler spreads. Our approach depends on the mathematical properties of ZC sequences in the DD domain. We derive a closed form expression for ZC pilots in the DD domain, we characterize the possible self-ambiguity functions, and we determine the magnitude of the possible cross-ambiguity functions. These mathematical properties enable detection of multiple pilots through solution of a compressed sensing problem. The columns of the compressed sensing matrix are the translates of individual ZC pilots in delay and Doppler. We show that columns in the design matrix satisfy a coherence property that makes it possible to detect multiple preambles in a single Zak-OTFS subframe using One-Step Thresholding (OST), which is an algorithm with low complexity.

Zak-OTFS and LDPC Codes

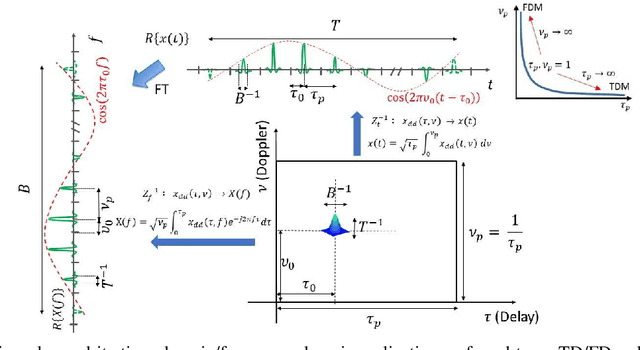
Orthogonal Time Frequency Space (OTFS) is a framework for communications and active sensing that processes signals in the delay-Doppler (DD) domain. It is informed by 6G propagation environments, where Doppler spreads measured in kHz make it more and more difficult to estimate channels, and the standard model-dependent approach to wireless communication is starting to break down. We consider Zak-OTFS where inverse Zak transform converts information symbols mounted on DD domain pulses to the time domain for transmission. Zak-OTFS modulation is parameterized by a delay period $\tau_{p}$ and a Doppler period $\nu_{p}$, where the product $\tau_{p}\nu_{p}=1$. When the channel spread is less than the delay period, and the Doppler spread is less than the Doppler period, the Zak-OTFS input-output relation can be predicted from the response to a single pilot symbol. The highly reliable channel estimates concentrate around the pilot location, and we configure low-density parity-check (LDPC) codes that take advantage of this prior information about reliability. It is advantageous to allocate information symbols to more reliable bins in the DD domain. We report simulation results for a Veh-A channel model where it is not possible to resolve all the paths, showing that LDPC coding extends the range of Doppler spreads for which reliable model-free communication is possible. We show that LDPC coding reduces sensitivity to the choice of transmit filter, making bandwidth expansion less necessary. Finally, we compare BER performance of Zak-OTFS to that of a multicarrier approximation (MC-OTFS), showing LDPC coding amplifies the gains previously reported for uncoded transmission.

Unequal Error Protection Achieves Threshold Gains on BEC and BSC via Higher Fidelity Messages

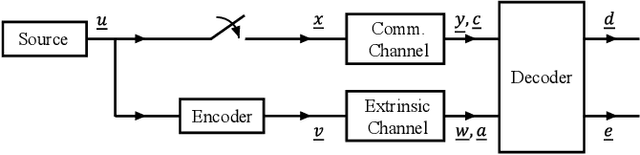
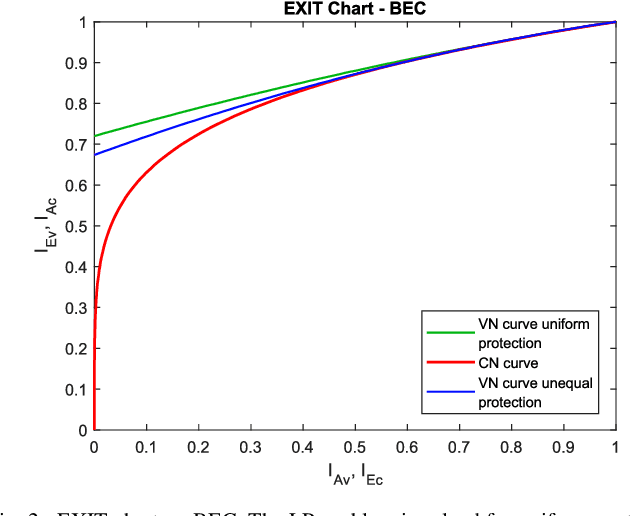
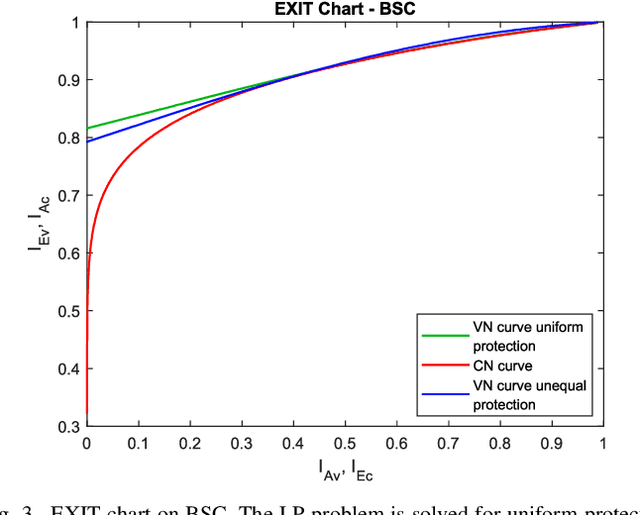
Because of their capacity-approaching performance, graph-based codes have a wide range of applications, including communications and storage. In these codes, unequal error protection (UEP) can offer performance gains with limited rate loss. Recent empirical results in magnetic recording (MR) systems show that extra protection for the parity bits of a low-density parity-check (LDPC) code via constrained coding results in significant density gains. In particular, when UEP is applied via more reliable parity bits, higher fidelity messages of parity bits are spread to all bits by message passing algorithm, enabling performance gains. Threshold analysis is a tool to measure the effectiveness of a graph-based code or coding scheme. In this paper, we provide a theoretical analysis of this UEP idea using extrinsic information transfer (EXIT) charts in the binary erasure channel (BEC) and the binary symmetric channel (BSC). We use EXIT functions to investigate the effect of change in mutual information of parity bits on the overall coding scheme. We propose a setup in which parity bits of a repeat-accumulate (RA) LDPC code have lower erasure or crossover probabilities than input information bits. We derive the a-priori and extrinsic mutual information functions for check nodes and variable nodes of the code. After applying our UEP setup to the information functions, we formulate a linear programming problem to find the optimal degree distribution that maximizes the code rate under the decoding convergence constraint. Results show that UEP via higher fidelity parity bits achieves up to about $17\%$ and $28\%$ threshold gains on BEC and BSC, respectively.