Unequal Error Protection Achieves Threshold Gains on BEC and BSC via Higher Fidelity Messages
Paper and Code
Jan 22, 2021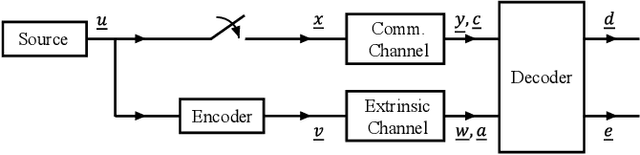
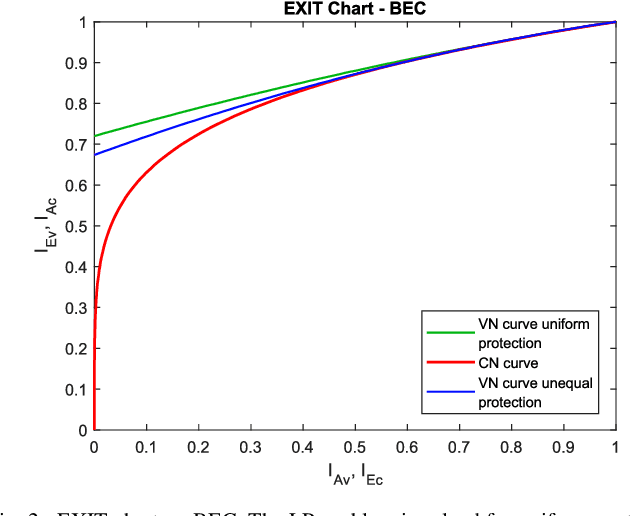
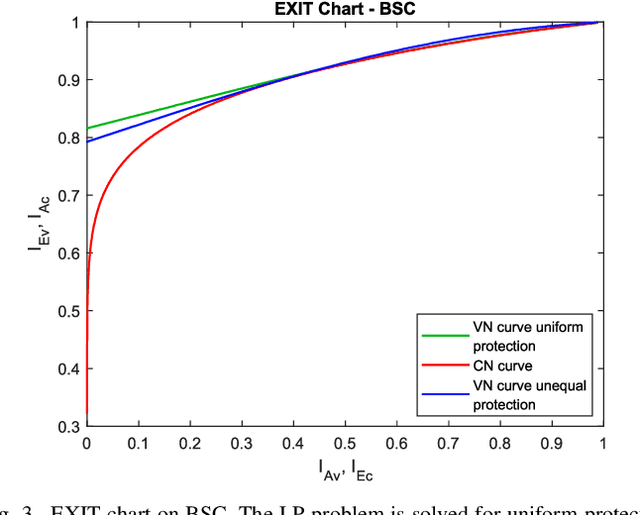

Because of their capacity-approaching performance, graph-based codes have a wide range of applications, including communications and storage. In these codes, unequal error protection (UEP) can offer performance gains with limited rate loss. Recent empirical results in magnetic recording (MR) systems show that extra protection for the parity bits of a low-density parity-check (LDPC) code via constrained coding results in significant density gains. In particular, when UEP is applied via more reliable parity bits, higher fidelity messages of parity bits are spread to all bits by message passing algorithm, enabling performance gains. Threshold analysis is a tool to measure the effectiveness of a graph-based code or coding scheme. In this paper, we provide a theoretical analysis of this UEP idea using extrinsic information transfer (EXIT) charts in the binary erasure channel (BEC) and the binary symmetric channel (BSC). We use EXIT functions to investigate the effect of change in mutual information of parity bits on the overall coding scheme. We propose a setup in which parity bits of a repeat-accumulate (RA) LDPC code have lower erasure or crossover probabilities than input information bits. We derive the a-priori and extrinsic mutual information functions for check nodes and variable nodes of the code. After applying our UEP setup to the information functions, we formulate a linear programming problem to find the optimal degree distribution that maximizes the code rate under the decoding convergence constraint. Results show that UEP via higher fidelity parity bits achieves up to about $17\%$ and $28\%$ threshold gains on BEC and BSC, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge