Probabilistic Design of Multi-Dimensional Spatially-Coupled Codes

Because of their excellent asymptotic and finite-length performance, spatially-coupled (SC) codes are a class of low-density parity-check codes that is gaining increasing attention. Multi-dimensional (MD) SC codes are constructed by connecting copies of an SC code via relocations in order to mitigate various sources of non-uniformity and improve performance in many data storage and data transmission systems. As the number of degrees of freedom in the MD-SC code design increases, appropriately exploiting them becomes more difficult because of the complexity growth of the design process. In this paper, we propose a probabilistic framework for the MD-SC code design, which is based on the gradient-descent (GD) algorithm, to design better MD codes and address this challenge. In particular, we express the expected number of short cycles, which we seek to minimize, in the graph representation of the code in terms of entries of a probability-distribution matrix that characterizes the MD-SC code design. We then find a locally-optimal probability distribution, which serves as the starting point of a finite-length algorithmic optimizer that produces the final MD-SC code. We offer the theoretical analysis as well as the algorithms, and we present experimental results demonstrating that our MD codes, conveniently called GD-MD codes, have notably lower short cycle numbers compared with the available state-of-the-art. Moreover, our algorithms converge on solutions in few iterations, which confirms the complexity reduction as a result of limiting the search space via the locally-optimal GD-MD distributions.

Protecting the Future of Information: LOCO Coding With Error Detection for DNA Data Storage

DNA strands serve as a storage medium for $4$-ary data over the alphabet $\{A,T,G,C\}$. DNA data storage promises formidable information density, long-term durability, and ease of replicability. However, information in this intriguing storage technology might be corrupted. Experiments have revealed that DNA sequences with long homopolymers and/or with low $GC$-content are notably more subject to errors upon storage. This paper investigates the utilization of the recently-introduced method for designing lexicographically-ordered constrained (LOCO) codes in DNA data storage. This paper introduces DNA LOCO (D-LOCO) codes, over the alphabet $\{A,T,G,C\}$ with limited runs of identical symbols. These codes come with an encoding-decoding rule we derive, which provides affordable encoding-decoding algorithms. In terms of storage overhead, the proposed encoding-decoding algorithms outperform those in the existing literature. Our algorithms are readily reconfigurable. D-LOCO codes are intrinsically balanced, which allows us to achieve balancing over the entire DNA strand with minimal rate penalty. Moreover, we propose four schemes to bridge consecutive codewords, three of which guarantee single substitution error detection per codeword. We examine the probability of undetecting errors. We also show that D-LOCO codes are capacity-achieving and that they offer remarkably high rates at moderate lengths.

Eliminating Media Noise While Preserving Storage Capacity: Reconfigurable Constrained Codes for Two-Dimensional Magnetic Recording

Magnetic recording devices are still competitive in the storage density race with solid-state devices thanks to new technologies such as two-dimensional magnetic recording (TDMR). Advanced data processing schemes are needed to guarantee reliability in TDMR. Data patterns where a bit is surrounded by complementary bits at the four positions with Manhattan distance $1$ on the TDMR grid are called plus isolation (PIS) patterns, and they are error-prone. Recently, we introduced lexicographically-ordered constrained (LOCO) codes, namely optimal plus LOCO (OP-LOCO) codes, that prevent these patterns from being written in a TDMR device. However, in the high-density regime or the low-energy regime, additional error-prone patterns emerge, specifically data patterns where a bit is surrounded by complementary bits at only three positions with Manhattan distance $1$, and we call them incomplete plus isolation (IPIS) patterns. In this paper, we present capacity-achieving codes that forbid both PIS and IPIS patterns in TDMR systems with wide read heads. We collectively call the PIS and IPIS patterns rotated T isolation (RTIS) patterns, and we call the new codes optimal T LOCO (OT-LOCO) codes. We analyze OT-LOCO codes and present their simple encoding-decoding rule that allows reconfigurability. We also present a novel bridging idea for these codes to further increase the rate. Our simulation results demonstrate that OT-LOCO codes are capable of eliminating media noise effects entirely at practical TD densities with high rates. To further preserve the storage capacity, we suggest using OP-LOCO codes early in the device lifetime, then employing the reconfiguration property to switch to OT-LOCO codes later. While the point of reconfiguration on the density/energy axis is decided manually at the moment, the next step is to use machine learning to take that decision based on the TDMR device status.

Efficient Constrained Codes That Enable Page Separation in Modern Flash Memories

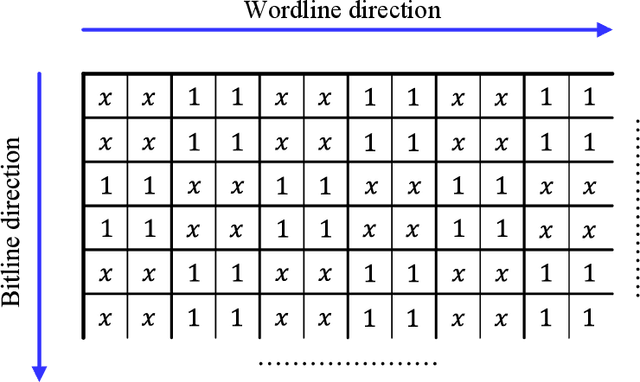
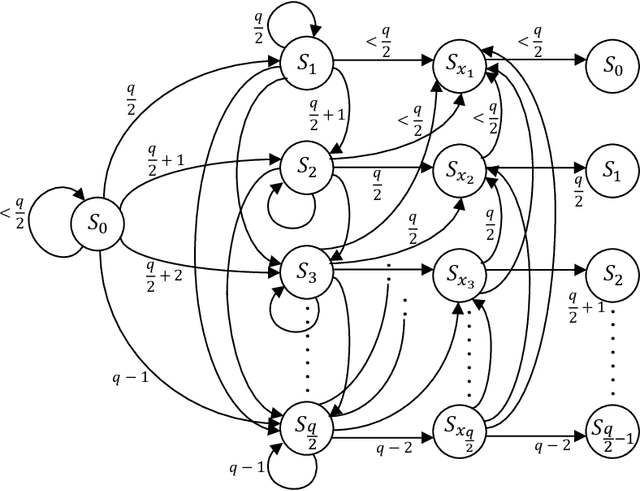
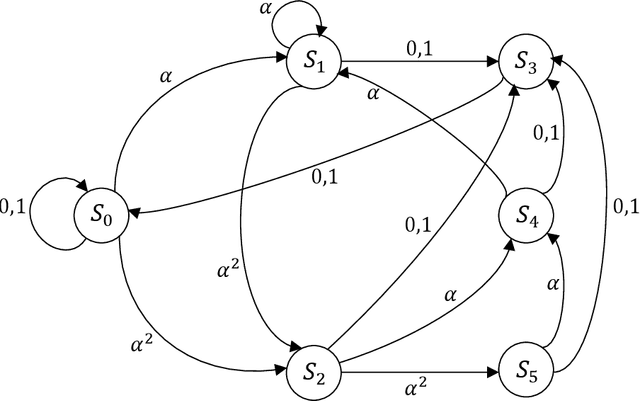
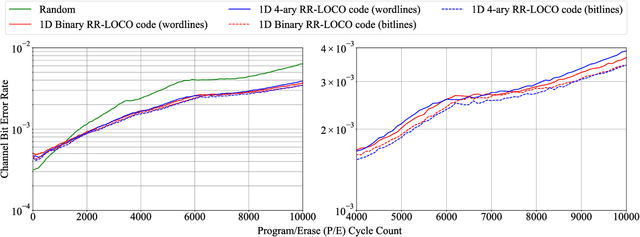
The pivotal storage density win achieved by solid-state devices over magnetic devices recently is a result of multiple innovations in physics, architecture, and signal processing. Constrained coding is used in Flash devices to increase reliability via mitigating inter-cell interference. Recently, capacity-achieving constrained codes were introduced to serve that purpose. While these codes result in minimal redundancy, they result in non-negligible complexity increase and access speed limitation since pages cannot be read separately. In this paper, we suggest new constrained coding schemes that have low-complexity and preserve the desirable high access speed in modern Flash devices. The idea is to eliminate error-prone patterns by coding data either only on the left-most page (binary coding) or only on the two left-most pages ($4$-ary coding) while leaving data on all the remaining pages uncoded. Our coding schemes are systematic and capacity-approaching. We refer to the proposed schemes as read-and-run (RR) constrained coding schemes. The $4$-ary RR coding scheme is introduced to limit the rate loss. We analyze the new RR coding schemes and discuss their impact on the probability of occurrence of different charge levels. We also demonstrate the performance improvement achieved via RR coding on a practical triple-level cell Flash device.

Read-and-Run Constrained Coding for Modern Flash Devices

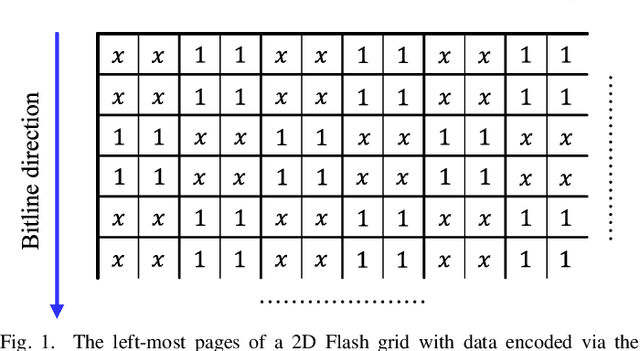
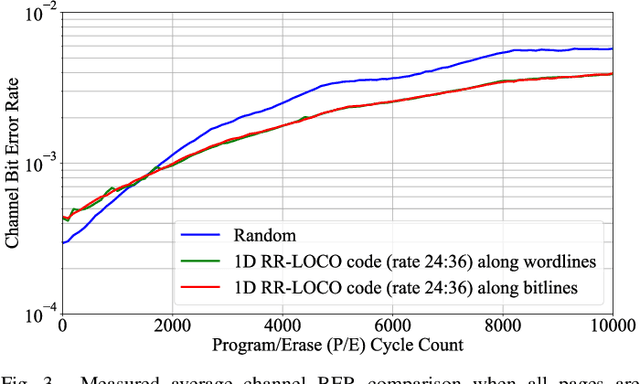
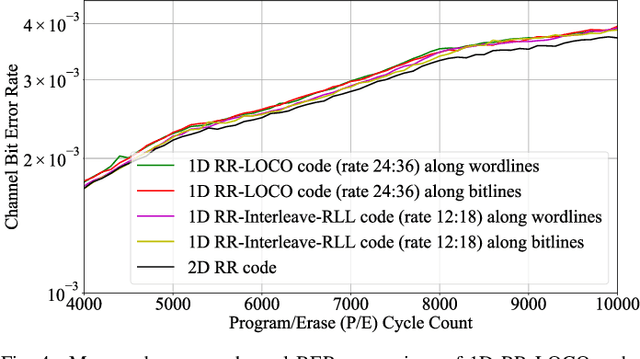
The pivotal storage density win achieved by solid-state devices over magnetic devices in 2015 is a result of multiple innovations in physics, architecture, and signal processing. One of the most important innovations in that regard is enabling the storage of more than one bit per cell in the Flash device, i.e., having more than two charge levels per cell. Constrained coding is used in Flash devices to increase reliability via mitigating inter-cell interference that stems from charge propagation among cells. Recently, capacity-achieving constrained codes were introduced to serve that purpose in modern Flash devices, which have more than two levels per cell. While these codes result in minimal redundancy via exploiting the underlying physics, they result in non-negligible complexity increase and access speed limitation since pages cannot be read separately. In this paper, we suggest new constrained coding schemes that have low-complexity and preserve the desirable high access speed in modern Flash devices. The idea is to eliminate error-prone patterns by coding data only on the left-most page while leaving data on all the remaining pages uncoded. Our coding schemes work for any number of levels per cell, offer systematic encoding and decoding, and are capacity-approaching. Since the proposed schemes enable the separation of pages, we refer to them as read-and-run (RR) constrained coding schemes as opposed to schemes adopting read-and-wait for other pages. We analyze the new RR coding schemes and discuss their impact on the probability of occurrence of different charge levels. We also demonstrate the performance improvement achieved via RR coding on a practical triple-level cell Flash device.

Unequal Error Protection Achieves Threshold Gains on BEC and BSC via Higher Fidelity Messages

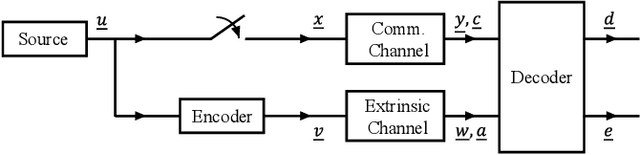
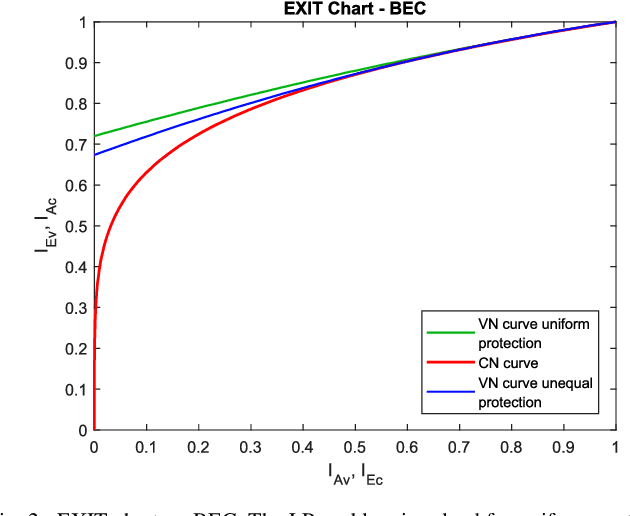
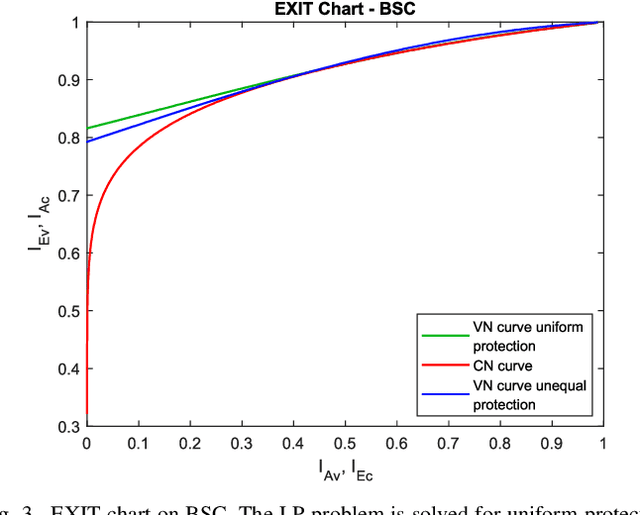
Because of their capacity-approaching performance, graph-based codes have a wide range of applications, including communications and storage. In these codes, unequal error protection (UEP) can offer performance gains with limited rate loss. Recent empirical results in magnetic recording (MR) systems show that extra protection for the parity bits of a low-density parity-check (LDPC) code via constrained coding results in significant density gains. In particular, when UEP is applied via more reliable parity bits, higher fidelity messages of parity bits are spread to all bits by message passing algorithm, enabling performance gains. Threshold analysis is a tool to measure the effectiveness of a graph-based code or coding scheme. In this paper, we provide a theoretical analysis of this UEP idea using extrinsic information transfer (EXIT) charts in the binary erasure channel (BEC) and the binary symmetric channel (BSC). We use EXIT functions to investigate the effect of change in mutual information of parity bits on the overall coding scheme. We propose a setup in which parity bits of a repeat-accumulate (RA) LDPC code have lower erasure or crossover probabilities than input information bits. We derive the a-priori and extrinsic mutual information functions for check nodes and variable nodes of the code. After applying our UEP setup to the information functions, we formulate a linear programming problem to find the optimal degree distribution that maximizes the code rate under the decoding convergence constraint. Results show that UEP via higher fidelity parity bits achieves up to about $17\%$ and $28\%$ threshold gains on BEC and BSC, respectively.