Locating Information in Large Language Models via Random Matrix Theory

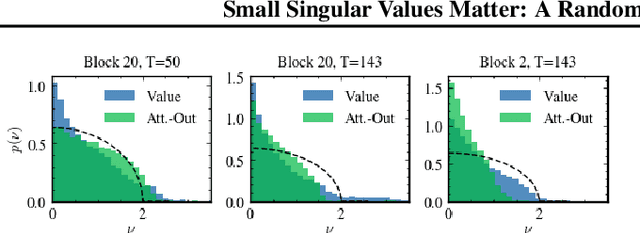
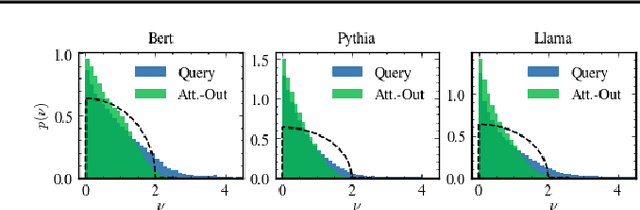
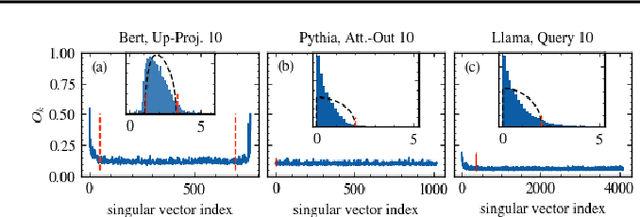
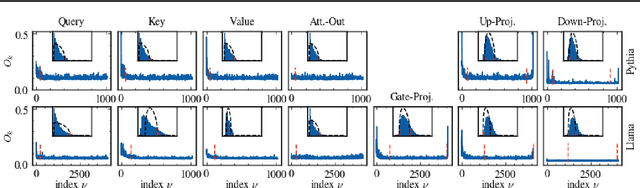
As large language models (LLMs) become central to AI applications, gaining a deeper understanding of their inner workings is increasingly important. In this work, we analyze the weight matrices of pretrained transformer models -- specifically BERT and Llama -- using random matrix theory (RMT) as a zero-information hypothesis. While randomly initialized weights perfectly agree with RMT predictions, deviations emerge after training, allowing us to locate learned structures within the models. We identify layer-type specific behaviors that are consistent across all blocks and architectures considered. By pinpointing regions that deviate from RMT predictions, we highlight areas of feature learning and confirm this through comparisons with the activation covariance matrices of the corresponding layers. Our method provides a diagnostic tool for identifying relevant regions in transformer weights using only the trained matrices. Additionally, we address the ongoing debate regarding the significance of small singular values in the context of fine-tuning and alignment in LLMs. Our findings reveal that, after fine-tuning, small singular values play a crucial role in the models' capabilities, suggesting that removing them in an already aligned transformer can be detrimental, as it may compromise model alignment.

Analyzing Neural Scaling Laws in Two-Layer Networks with Power-Law Data Spectra

Neural scaling laws describe how the performance of deep neural networks scales with key factors such as training data size, model complexity, and training time, often following power-law behaviors over multiple orders of magnitude. Despite their empirical observation, the theoretical understanding of these scaling laws remains limited. In this work, we employ techniques from statistical mechanics to analyze one-pass stochastic gradient descent within a student-teacher framework, where both the student and teacher are two-layer neural networks. Our study primarily focuses on the generalization error and its behavior in response to data covariance matrices that exhibit power-law spectra. For linear activation functions, we derive analytical expressions for the generalization error, exploring different learning regimes and identifying conditions under which power-law scaling emerges. Additionally, we extend our analysis to non-linear activation functions in the feature learning regime, investigating how power-law spectra in the data covariance matrix impact learning dynamics. Importantly, we find that the length of the symmetric plateau depends on the number of distinct eigenvalues of the data covariance matrix and the number of hidden units, demonstrating how these plateaus behave under various configurations. In addition, our results reveal a transition from exponential to power-law convergence in the specialized phase when the data covariance matrix possesses a power-law spectrum. This work contributes to the theoretical understanding of neural scaling laws and provides insights into optimizing learning performance in practical scenarios involving complex data structures.

Reevaluating Loss Functions: Enhancing Robustness to Label Noise in Deep Learning Models

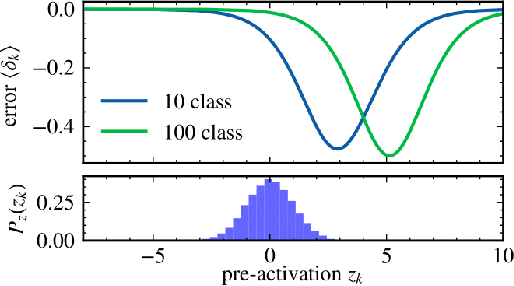
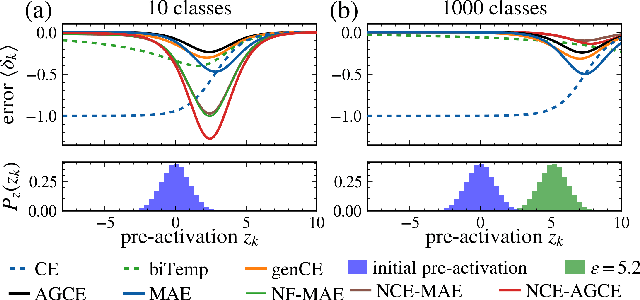
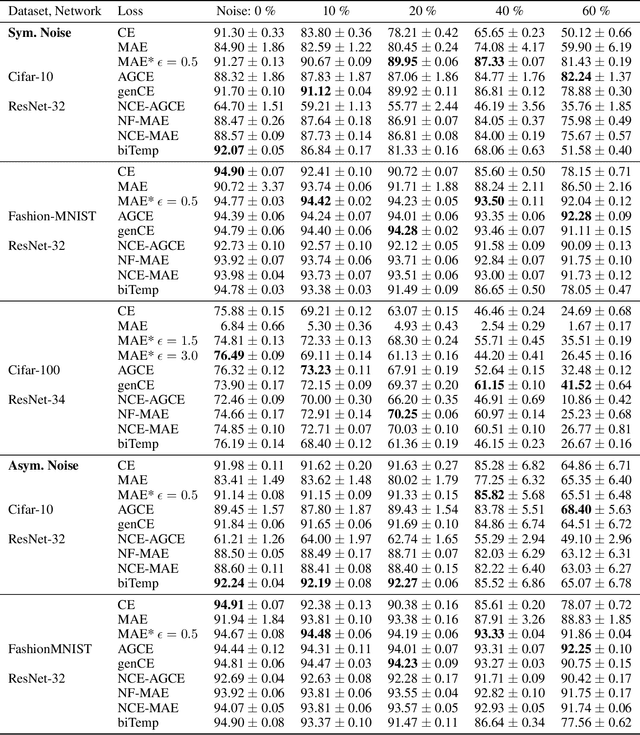
Large annotated datasets inevitably contain incorrect labels, which poses a major challenge for the training of deep neural networks as they easily fit the labels. Only when training with a robust model that is not easily distracted by the noise, a good generalization performance can be achieved. A simple yet effective way to create a noise robust model is to use a noise robust loss function. However, the number of proposed loss functions is large, they often come with hyperparameters, and may learn slower than the widely used but noise sensitive Cross Entropy loss. By heuristic considerations and extensive numerical experiments, we study in which situations the proposed loss functions are applicable and give suggestions on how to choose an appropriate loss. Additionally, we propose a novel technique to enhance learning with bounded loss functions: the inclusion of an output bias, i.e. a slight increase in the neuron pre-activation corresponding to the correct label. Surprisingly, we find that this not only significantly improves the learning of bounded losses, but also leads to the Mean Absolute Error loss outperforming the Cross Entropy loss on the Cifar-100 dataset - even in the absence of additional label noise. This suggests that training with a bounded loss function can be advantageous even in the presence of minimal label noise. To further strengthen our analysis of the learning behavior of different loss functions, we additionally design and test a novel loss function denoted as Bounded Cross Entropy.

Correlated Noise in Epoch-Based Stochastic Gradient Descent: Implications for Weight Variances

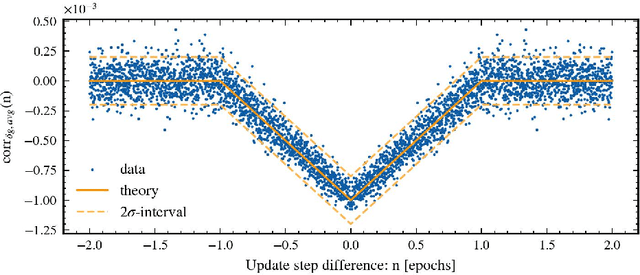
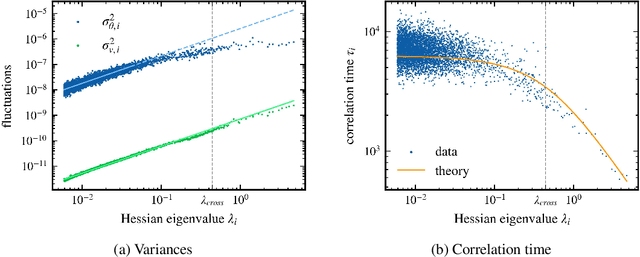
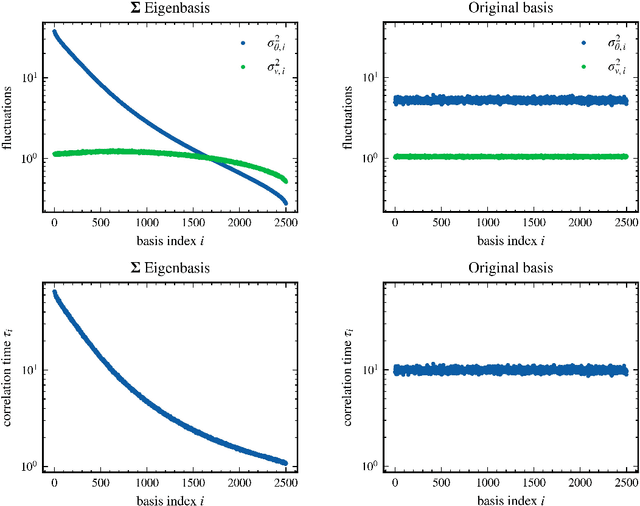
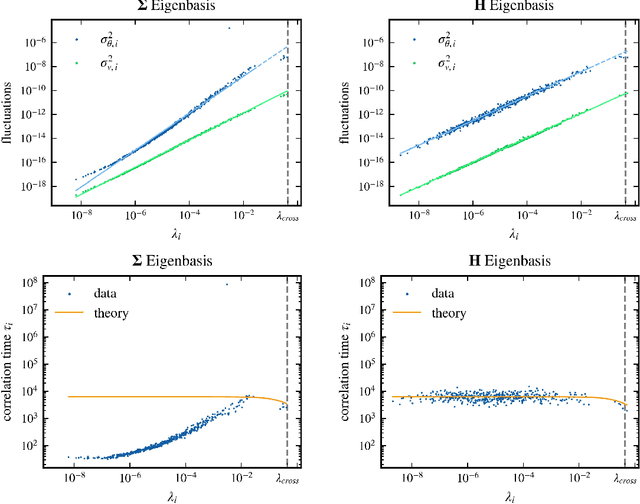
Stochastic gradient descent (SGD) has become a cornerstone of neural network optimization, yet the noise introduced by SGD is often assumed to be uncorrelated over time, despite the ubiquity of epoch-based training. In this work, we challenge this assumption and investigate the effects of epoch-based noise correlations on the stationary distribution of discrete-time SGD with momentum, limited to a quadratic loss. Our main contributions are twofold: first, we calculate the exact autocorrelation of the noise for training in epochs under the assumption that the noise is independent of small fluctuations in the weight vector; second, we explore the influence of correlations introduced by the epoch-based learning scheme on SGD dynamics. We find that for directions with a curvature greater than a hyperparameter-dependent crossover value, the results for uncorrelated noise are recovered. However, for relatively flat directions, the weight variance is significantly reduced. We provide an intuitive explanation for these results based on a crossover between correlation times, contributing to a deeper understanding of the dynamics of SGD in the presence of epoch-based noise correlations.

Topological gap protocol based machine learning optimization of Majorana hybrid wires

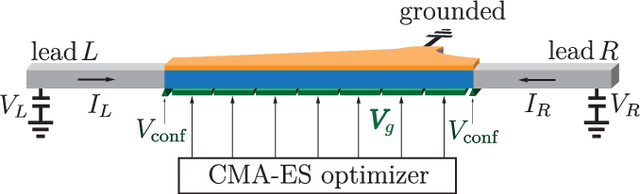
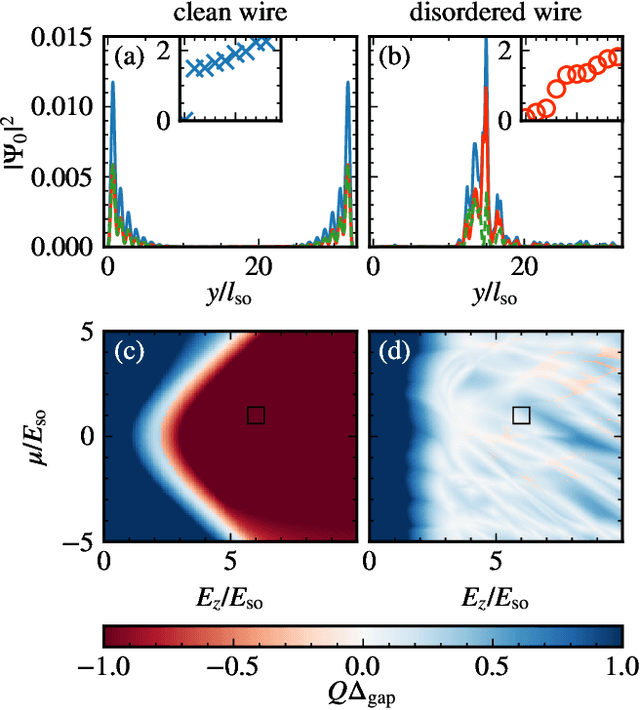
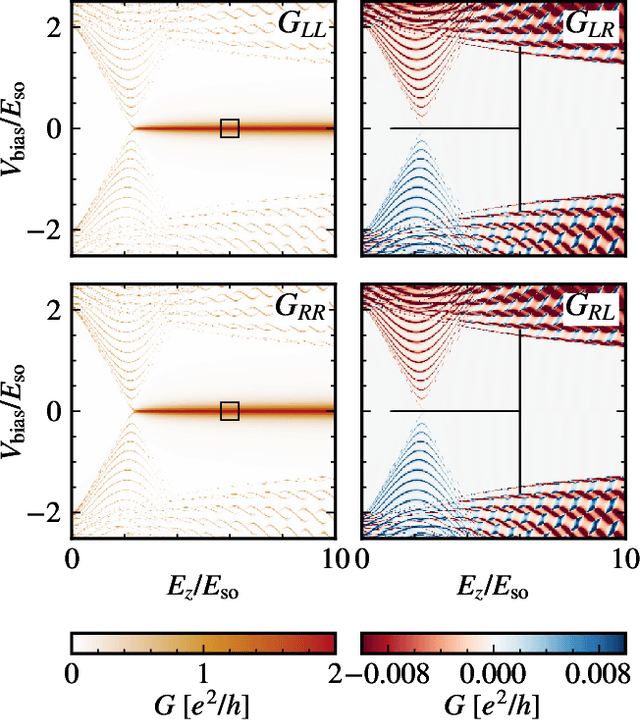
Majorana zero modes in superconductor-nanowire hybrid structures are a promising candidate for topologically protected qubits with the potential to be used in scalable structures. Currently, disorder in such Majorana wires is a major challenge, as it can destroy the topological phase and thus reduce the yield in the fabrication of Majorana devices. We study machine learning optimization of a gate array in proximity to a grounded Majorana wire, which allows us to reliably compensate even strong disorder. We propose a metric for optimization that is inspired by the topological gap protocol, and which can be implemented based on measurements of the non-local conductance through the wire.

Online Learning for the Random Feature Model in the Student-Teacher Framework

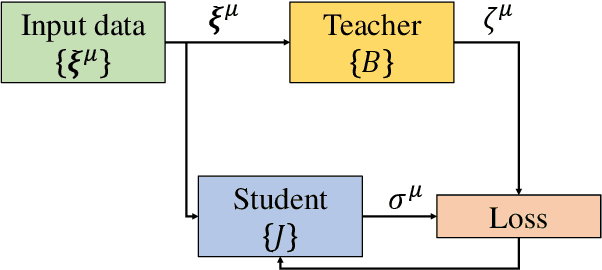
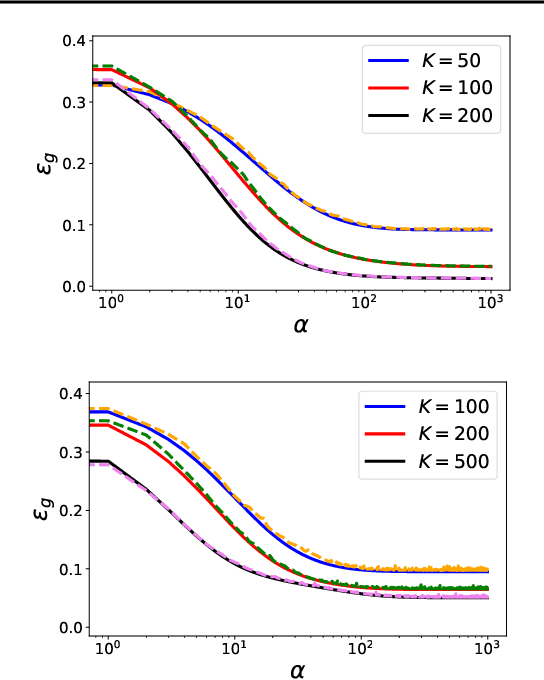
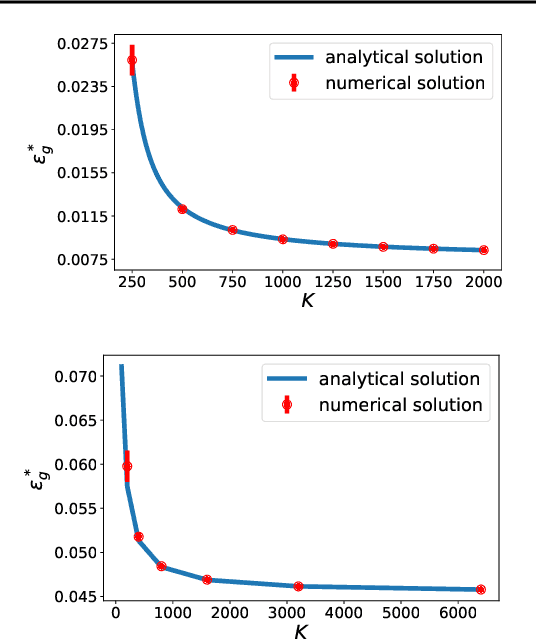
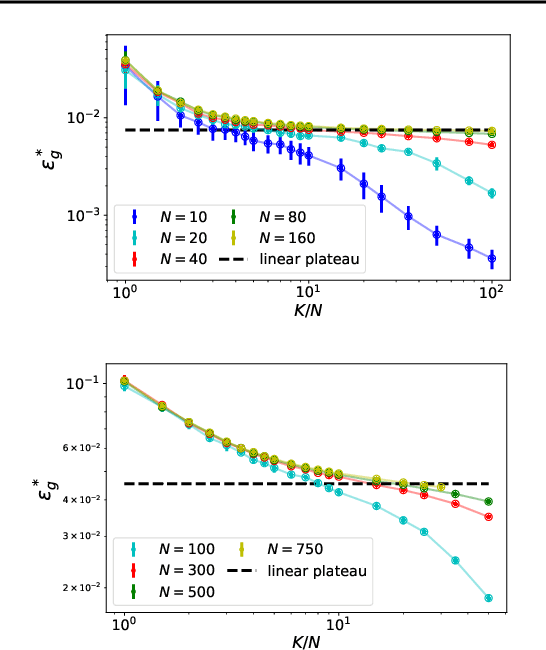
Deep neural networks are widely used prediction algorithms whose performance often improves as the number of weights increases, leading to over-parametrization. We consider a two-layered neural network whose first layer is frozen while the last layer is trainable, known as the random feature model. We study over-parametrization in the context of a student-teacher framework by deriving a set of differential equations for the learning dynamics. For any finite ratio of hidden layer size and input dimension, the student cannot generalize perfectly, and we compute the non-zero asymptotic generalization error. Only when the student's hidden layer size is exponentially larger than the input dimension, an approach to perfect generalization is possible.

Machine learning optimization of Majorana hybrid nanowires

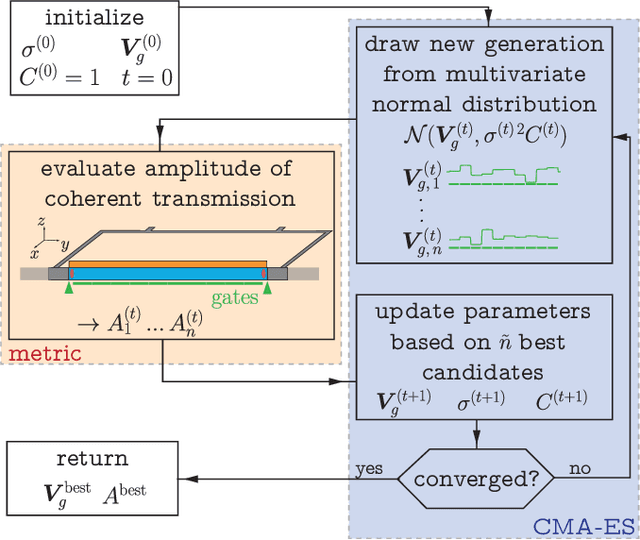
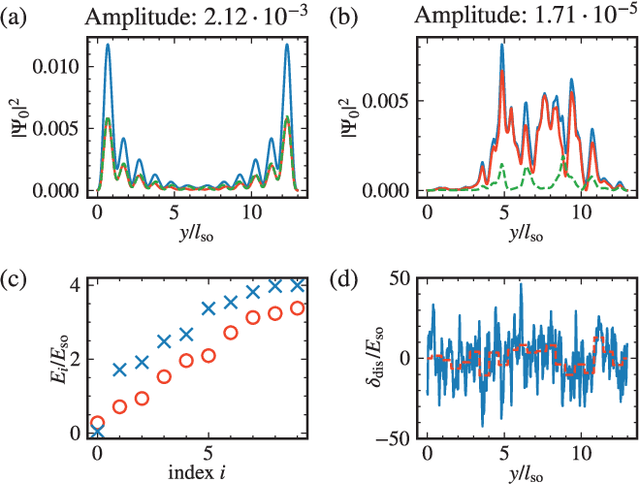
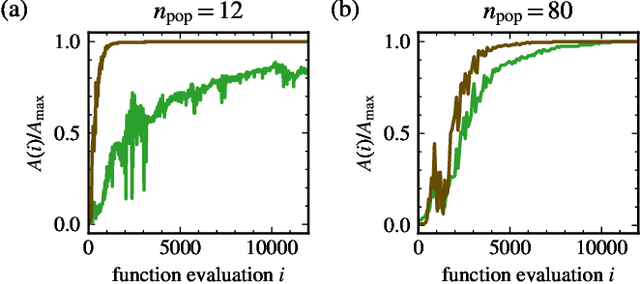
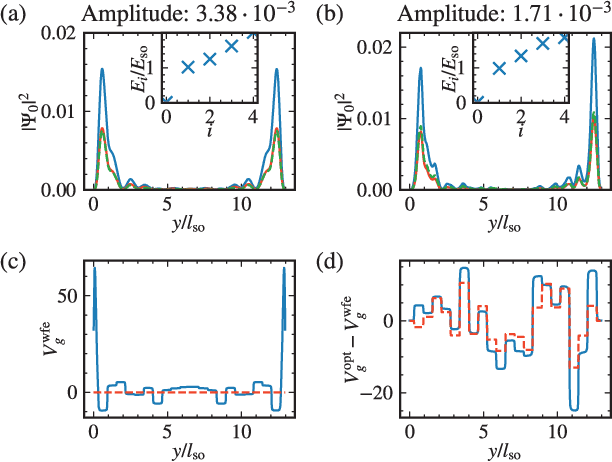
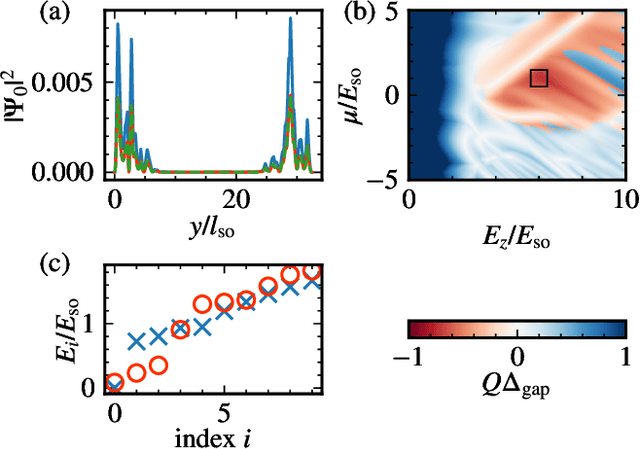
As the complexity of quantum systems such as quantum bit arrays increases, efforts to automate expensive tuning are increasingly worthwhile. We investigate machine learning based tuning of gate arrays using the CMA-ES algorithm for the case study of Majorana wires with strong disorder. We find that the algorithm is able to efficiently improve the topological signatures, learn intrinsic disorder profiles, and completely eliminate disorder effects. For example, with only 20 gates, it is possible to fully recover Majorana zero modes destroyed by disorder by optimizing gate voltages.

Boundary between noise and information applied to filtering neural network weight matrices

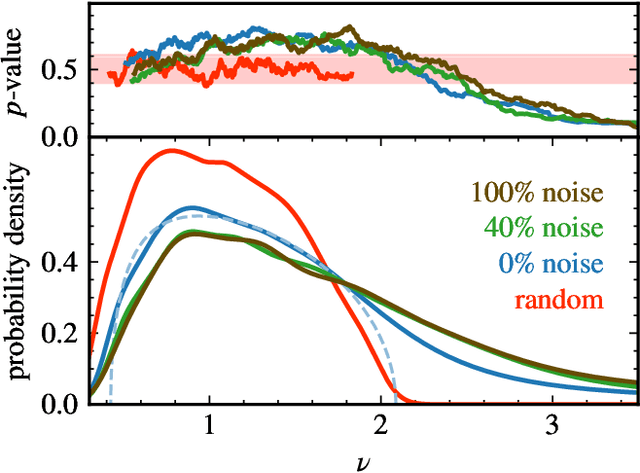
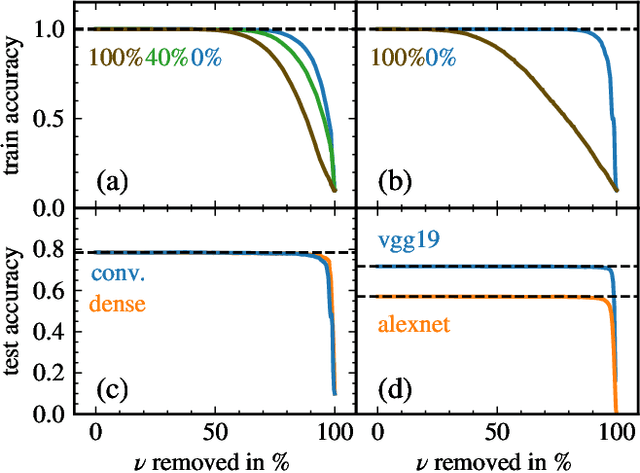
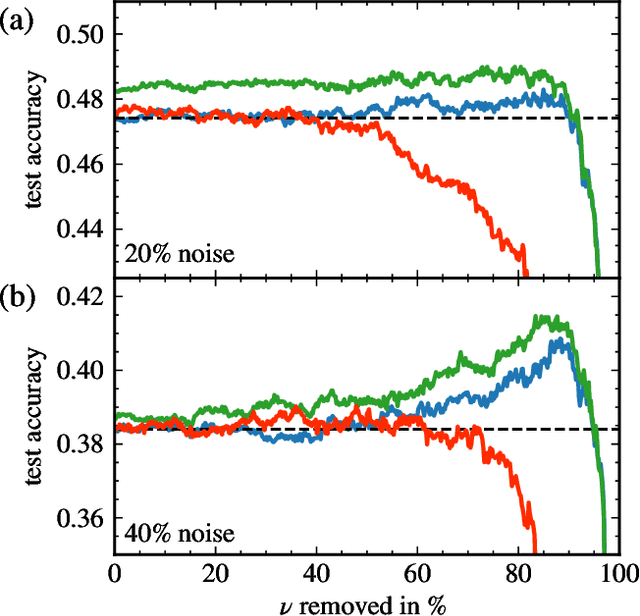
Deep neural networks have been successfully applied to a broad range of problems where overparametrization yields weight matrices which are partially random. A comparison of weight matrix singular vectors to the Porter-Thomas distribution suggests that there is a boundary between randomness and learned information in the singular value spectrum. Inspired by this finding, we introduce an algorithm for noise filtering, which both removes small singular values and reduces the magnitude of large singular values to counteract the effect of level repulsion between the noise and the information part of the spectrum. For networks trained in the presence of label noise, we indeed find that the generalization performance improves significantly due to noise filtering.

Random matrix analysis of deep neural network weight matrices

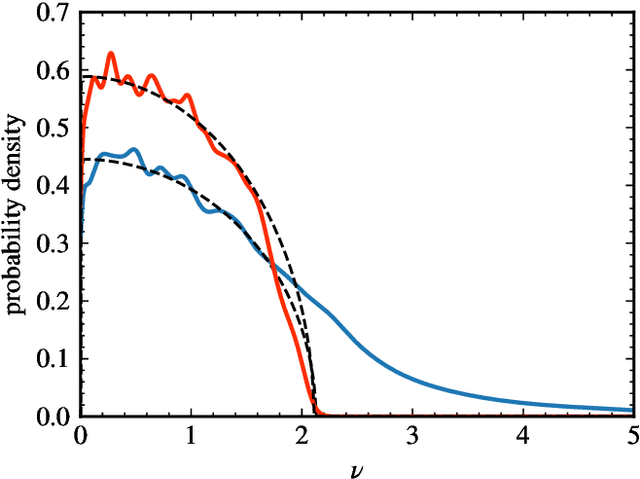
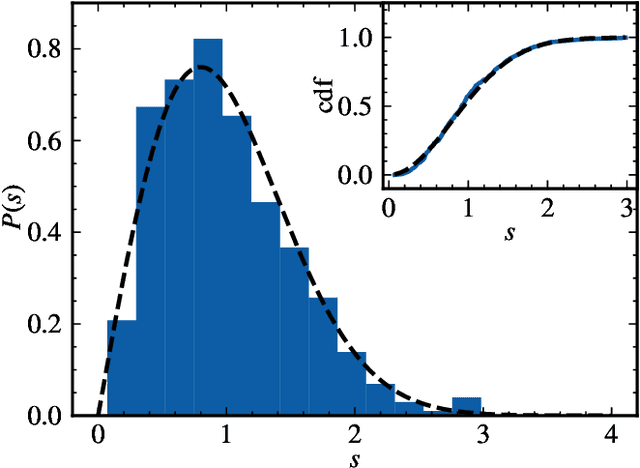
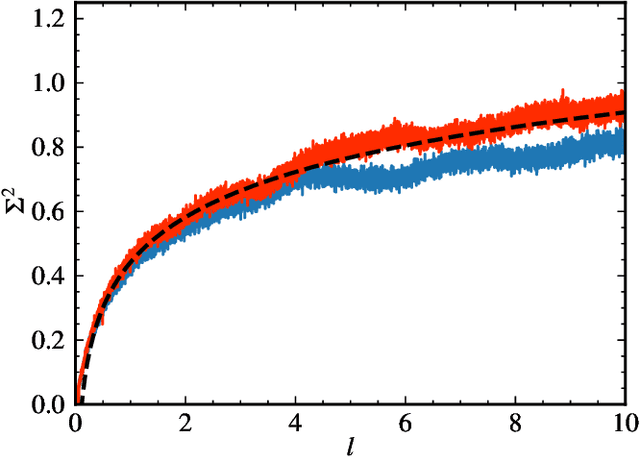
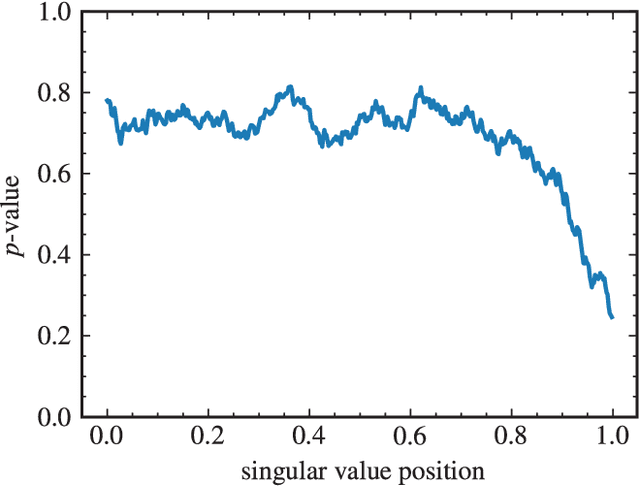
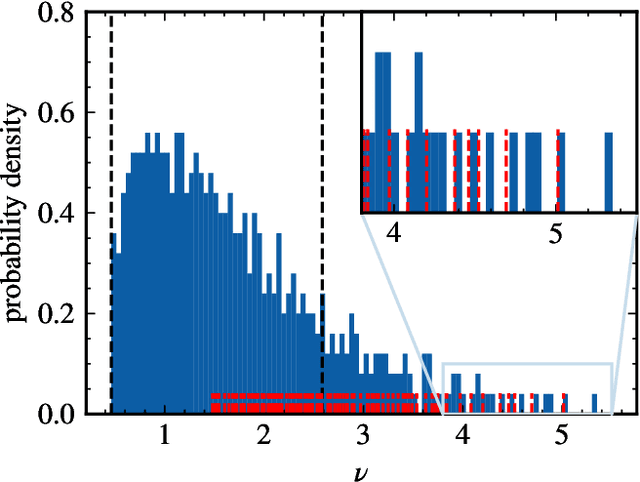
Neural networks have been used successfully in a variety of fields, which has led to a great deal of interest in developing a theoretical understanding of how they store the information needed to perform a particular task. We study the weight matrices of trained deep neural networks using methods from random matrix theory (RMT) and show that the statistics of most of the singular values follow universal RMT predictions. This suggests that they are random and do not contain system specific information, which we investigate further by comparing the statistics of eigenvector entries to the universal Porter-Thomas distribution. We find that for most eigenvectors the hypothesis of randomness cannot be rejected, and that only eigenvectors belonging to the largest singular values deviate from the RMT prediction, indicating that they may encode learned information. We analyze the spectral distribution of such large singular values using the Hill estimator and find that the distribution cannot be characterized by a tail index, i.e. is not of power law type.

Soft Mode in the Dynamics of Over-realizable On-line Learning for Soft Committee Machines

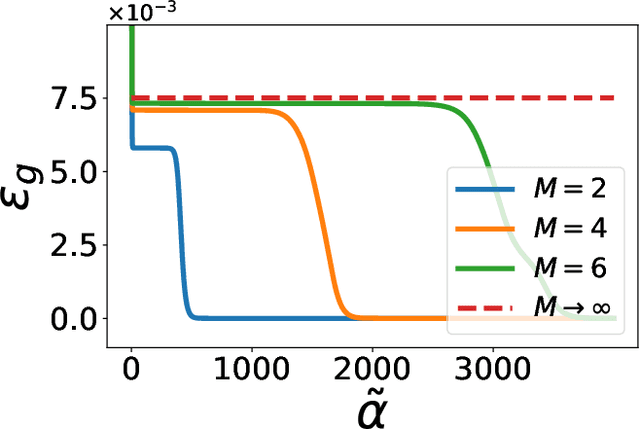
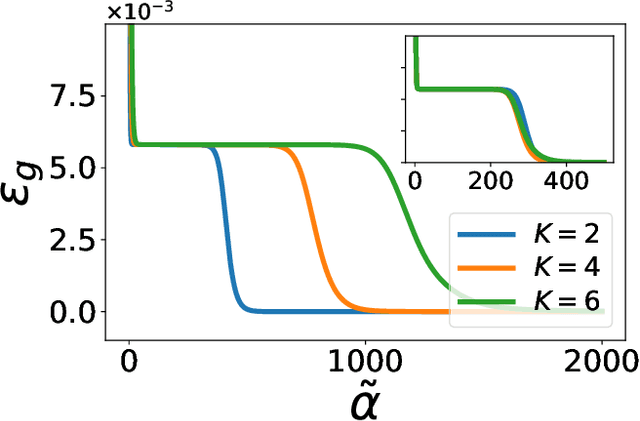
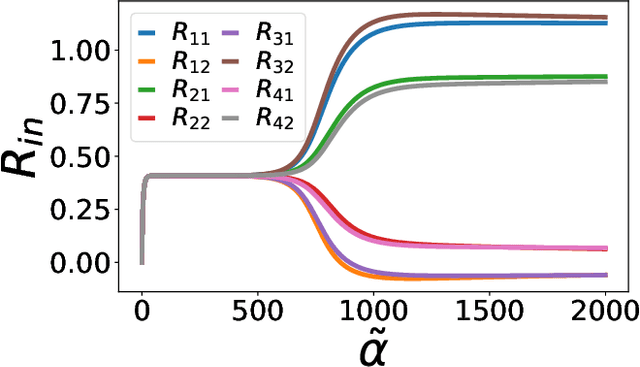
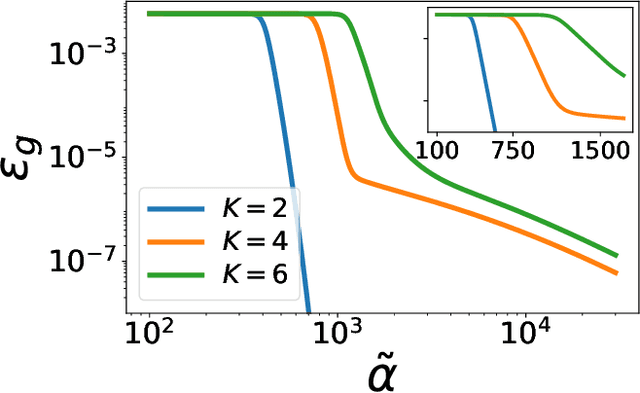
Over-parametrized deep neural networks trained by stochastic gradient descent are successful in performing many tasks of practical relevance. One aspect of over-parametrization is the possibility that the student network has a larger expressivity than the data generating process. In the context of a student-teacher scenario, this corresponds to the so-called over-realizable case, where the student network has a larger number of hidden units than the teacher. For on-line learning of a two-layer soft committee machine in the over-realizable case, we find that the approach to perfect learning occurs in a power-law fashion rather than exponentially as in the realizable case. All student nodes learn and replicate one of the teacher nodes if teacher and student outputs are suitably rescaled.