A Boundary-Layer Mechanism for One-Third Scaling in Online Softmax Classification

Hard-label classification is usually trained with smooth surrogate losses, most prominently softmax cross-entropy. We isolate an asymptotic mechanism by which this mismatch between smooth surrogate and discrete labels produces power-law learning curves in an online teacher-student model. After subtracting the mean logit, the thermodynamic-limit dynamics close in centered variables: a growing centered student-teacher alignment $D$ and the residual student variance $Δ$. At late times, examples away from teacher decision boundaries are already classified confidently and contribute exponentially little. Only boundary layers of width $O(D^{-1})$ remain active, while the noise of fixed-learning-rate online gradient descent maintains a nonzero $Δ$. As a function of the training time $α$ the late-time solution yields a $α^{-1/3}$ power law not only for the test loss but also for the generalization error $ε_g$, i.e., one minus test accuracy. This is much slower than the $α^{-1}$ Bayes-optimal reference for the same model. We further show that learning-rate schedules can improve the generalization error towards a $ε_g \sim α^{-1/2}$ power law. Simulations support the predicted order parameter dynamics and learning curves. Controlled experiments with correlated Gaussian inputs and whitened pretrained features show that data structure can dominate transients. Therefore, our result is an asymptotic, complementary mechanism rather than an alternative to spectral explanations of neural scaling laws.

Correlated Noise in Epoch-Based Stochastic Gradient Descent: Implications for Weight Variances

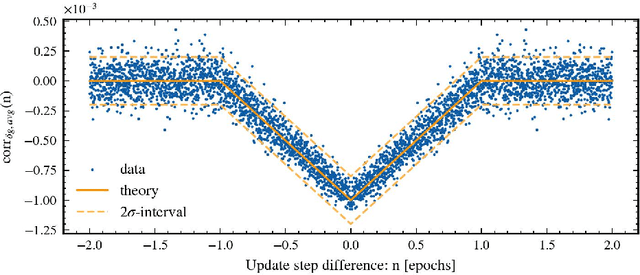
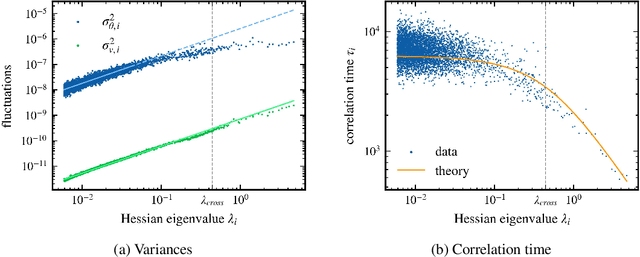
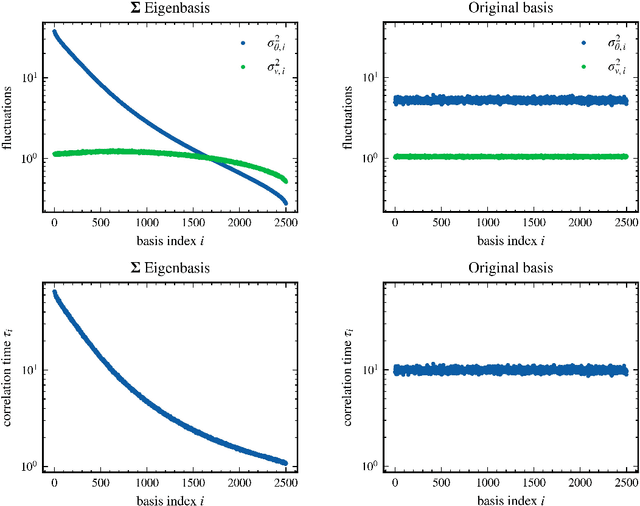
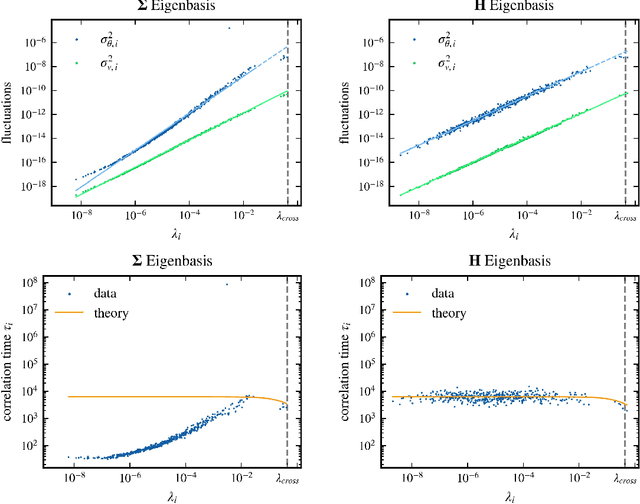
Stochastic gradient descent (SGD) has become a cornerstone of neural network optimization, yet the noise introduced by SGD is often assumed to be uncorrelated over time, despite the ubiquity of epoch-based training. In this work, we challenge this assumption and investigate the effects of epoch-based noise correlations on the stationary distribution of discrete-time SGD with momentum, limited to a quadratic loss. Our main contributions are twofold: first, we calculate the exact autocorrelation of the noise for training in epochs under the assumption that the noise is independent of small fluctuations in the weight vector; second, we explore the influence of correlations introduced by the epoch-based learning scheme on SGD dynamics. We find that for directions with a curvature greater than a hyperparameter-dependent crossover value, the results for uncorrelated noise are recovered. However, for relatively flat directions, the weight variance is significantly reduced. We provide an intuitive explanation for these results based on a crossover between correlation times, contributing to a deeper understanding of the dynamics of SGD in the presence of epoch-based noise correlations.