Locating Information in Large Language Models via Random Matrix Theory

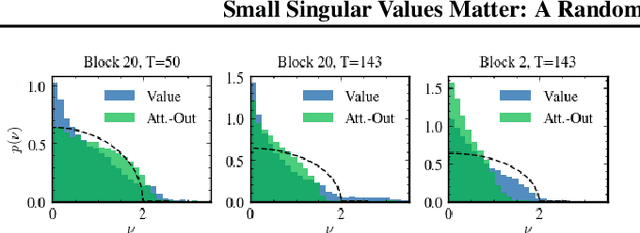
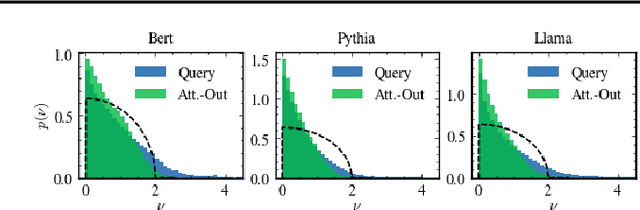
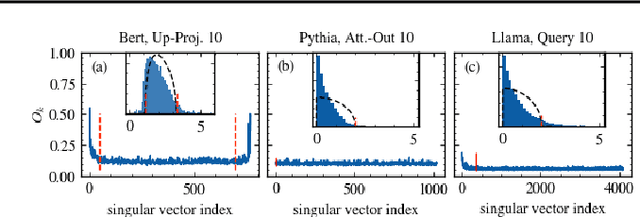
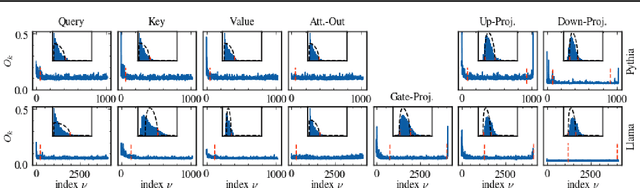
As large language models (LLMs) become central to AI applications, gaining a deeper understanding of their inner workings is increasingly important. In this work, we analyze the weight matrices of pretrained transformer models -- specifically BERT and Llama -- using random matrix theory (RMT) as a zero-information hypothesis. While randomly initialized weights perfectly agree with RMT predictions, deviations emerge after training, allowing us to locate learned structures within the models. We identify layer-type specific behaviors that are consistent across all blocks and architectures considered. By pinpointing regions that deviate from RMT predictions, we highlight areas of feature learning and confirm this through comparisons with the activation covariance matrices of the corresponding layers. Our method provides a diagnostic tool for identifying relevant regions in transformer weights using only the trained matrices. Additionally, we address the ongoing debate regarding the significance of small singular values in the context of fine-tuning and alignment in LLMs. Our findings reveal that, after fine-tuning, small singular values play a crucial role in the models' capabilities, suggesting that removing them in an already aligned transformer can be detrimental, as it may compromise model alignment.

Reevaluating Loss Functions: Enhancing Robustness to Label Noise in Deep Learning Models

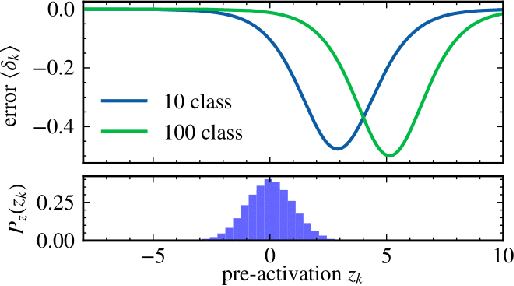
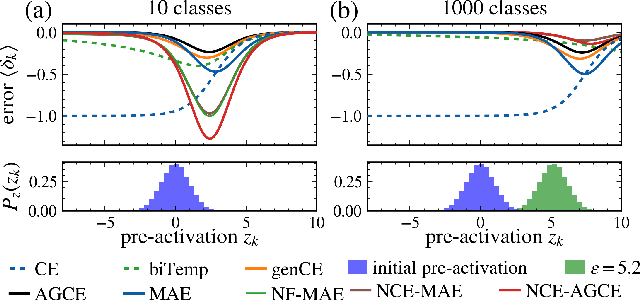
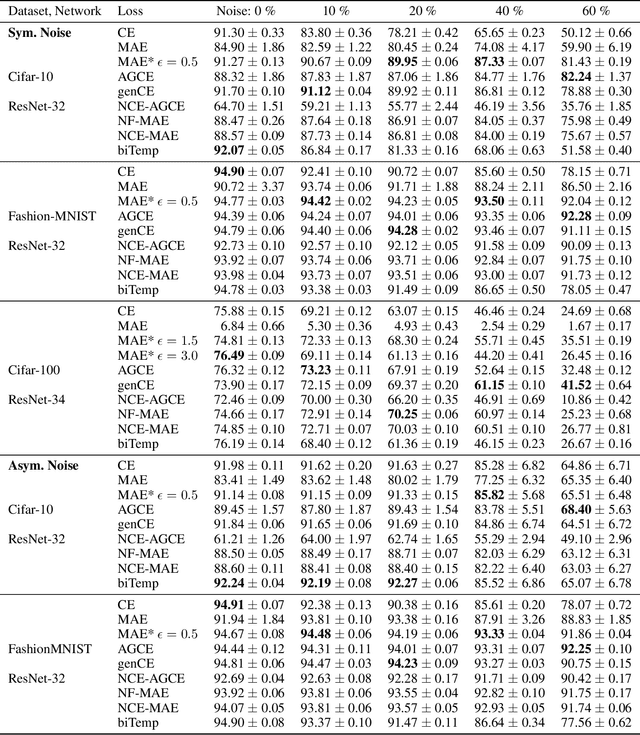
Large annotated datasets inevitably contain incorrect labels, which poses a major challenge for the training of deep neural networks as they easily fit the labels. Only when training with a robust model that is not easily distracted by the noise, a good generalization performance can be achieved. A simple yet effective way to create a noise robust model is to use a noise robust loss function. However, the number of proposed loss functions is large, they often come with hyperparameters, and may learn slower than the widely used but noise sensitive Cross Entropy loss. By heuristic considerations and extensive numerical experiments, we study in which situations the proposed loss functions are applicable and give suggestions on how to choose an appropriate loss. Additionally, we propose a novel technique to enhance learning with bounded loss functions: the inclusion of an output bias, i.e. a slight increase in the neuron pre-activation corresponding to the correct label. Surprisingly, we find that this not only significantly improves the learning of bounded losses, but also leads to the Mean Absolute Error loss outperforming the Cross Entropy loss on the Cifar-100 dataset - even in the absence of additional label noise. This suggests that training with a bounded loss function can be advantageous even in the presence of minimal label noise. To further strengthen our analysis of the learning behavior of different loss functions, we additionally design and test a novel loss function denoted as Bounded Cross Entropy.

Boundary between noise and information applied to filtering neural network weight matrices

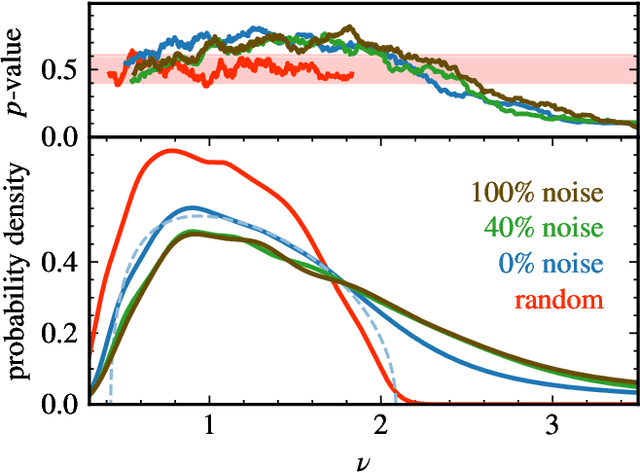
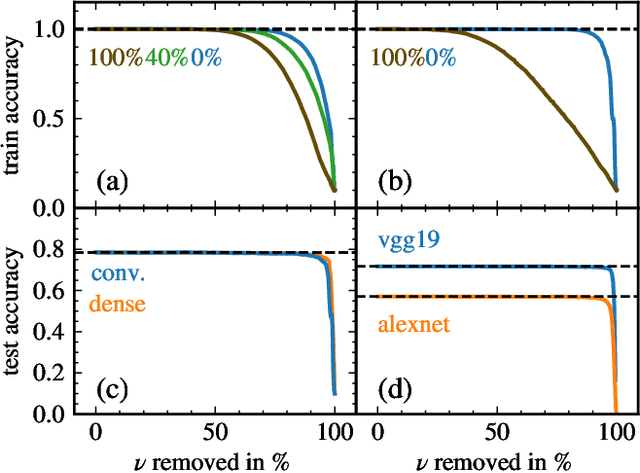
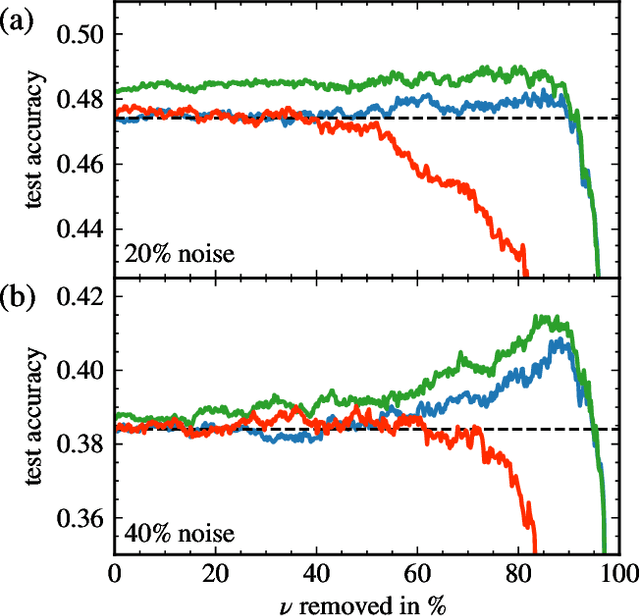
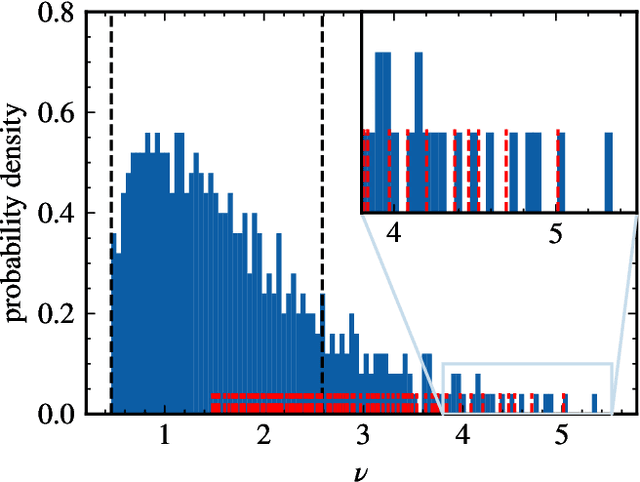
Deep neural networks have been successfully applied to a broad range of problems where overparametrization yields weight matrices which are partially random. A comparison of weight matrix singular vectors to the Porter-Thomas distribution suggests that there is a boundary between randomness and learned information in the singular value spectrum. Inspired by this finding, we introduce an algorithm for noise filtering, which both removes small singular values and reduces the magnitude of large singular values to counteract the effect of level repulsion between the noise and the information part of the spectrum. For networks trained in the presence of label noise, we indeed find that the generalization performance improves significantly due to noise filtering.

Random matrix analysis of deep neural network weight matrices

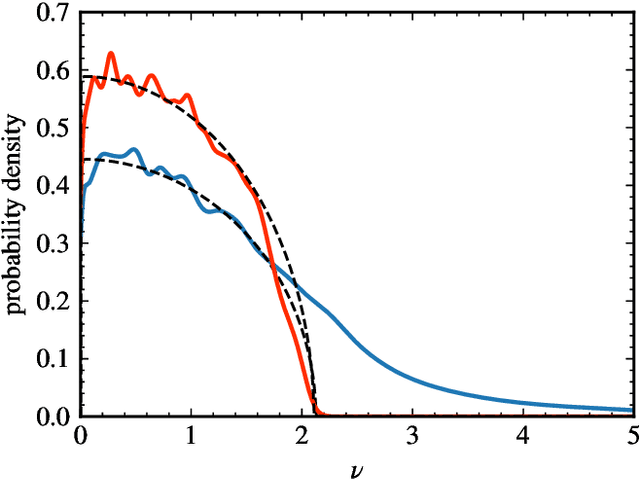
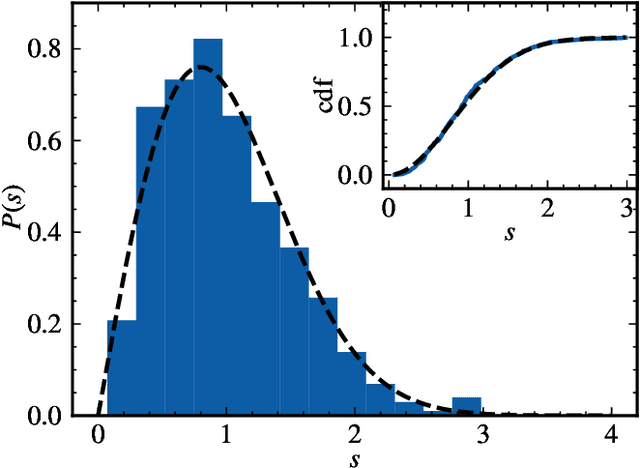
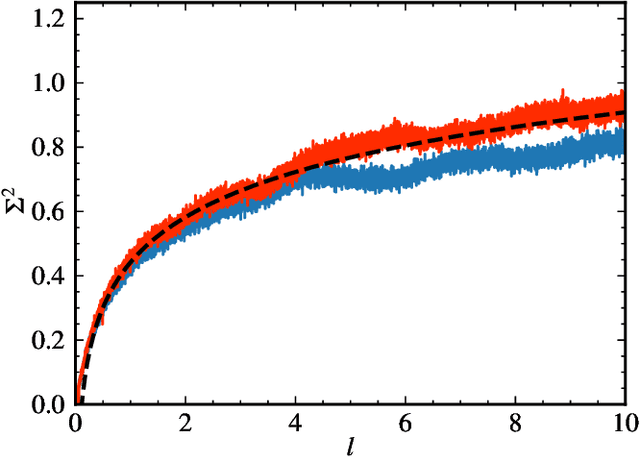
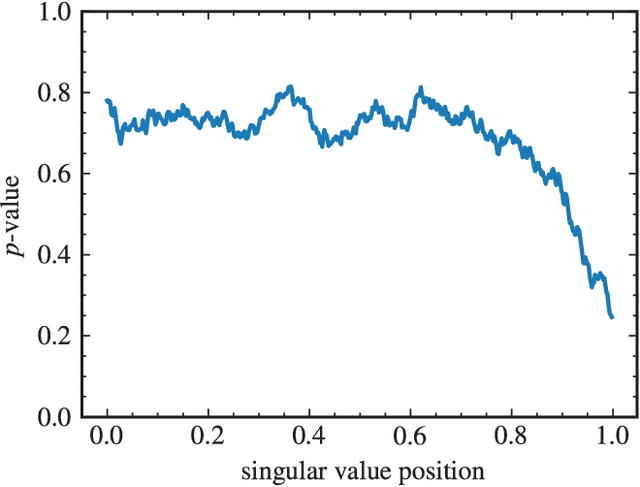
Neural networks have been used successfully in a variety of fields, which has led to a great deal of interest in developing a theoretical understanding of how they store the information needed to perform a particular task. We study the weight matrices of trained deep neural networks using methods from random matrix theory (RMT) and show that the statistics of most of the singular values follow universal RMT predictions. This suggests that they are random and do not contain system specific information, which we investigate further by comparing the statistics of eigenvector entries to the universal Porter-Thomas distribution. We find that for most eigenvectors the hypothesis of randomness cannot be rejected, and that only eigenvectors belonging to the largest singular values deviate from the RMT prediction, indicating that they may encode learned information. We analyze the spectral distribution of such large singular values using the Hill estimator and find that the distribution cannot be characterized by a tail index, i.e. is not of power law type.