Locating Information in Large Language Models via Random Matrix Theory
Paper and Code
Oct 23, 2024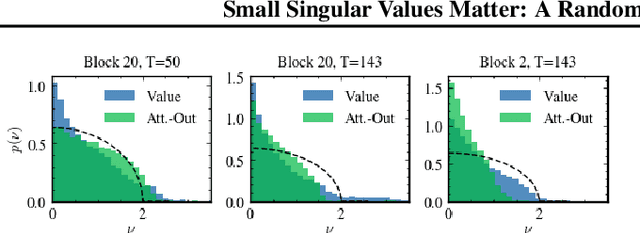
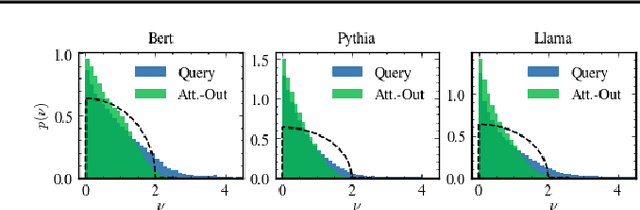
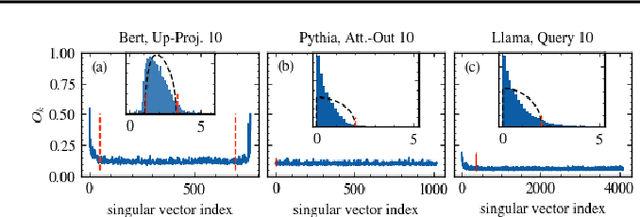
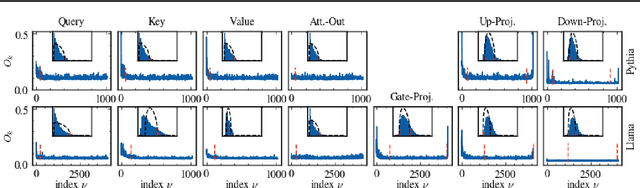
As large language models (LLMs) become central to AI applications, gaining a deeper understanding of their inner workings is increasingly important. In this work, we analyze the weight matrices of pretrained transformer models -- specifically BERT and Llama -- using random matrix theory (RMT) as a zero-information hypothesis. While randomly initialized weights perfectly agree with RMT predictions, deviations emerge after training, allowing us to locate learned structures within the models. We identify layer-type specific behaviors that are consistent across all blocks and architectures considered. By pinpointing regions that deviate from RMT predictions, we highlight areas of feature learning and confirm this through comparisons with the activation covariance matrices of the corresponding layers. Our method provides a diagnostic tool for identifying relevant regions in transformer weights using only the trained matrices. Additionally, we address the ongoing debate regarding the significance of small singular values in the context of fine-tuning and alignment in LLMs. Our findings reveal that, after fine-tuning, small singular values play a crucial role in the models' capabilities, suggesting that removing them in an already aligned transformer can be detrimental, as it may compromise model alignment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge