Analyzing Neural Scaling Laws in Two-Layer Networks with Power-Law Data Spectra

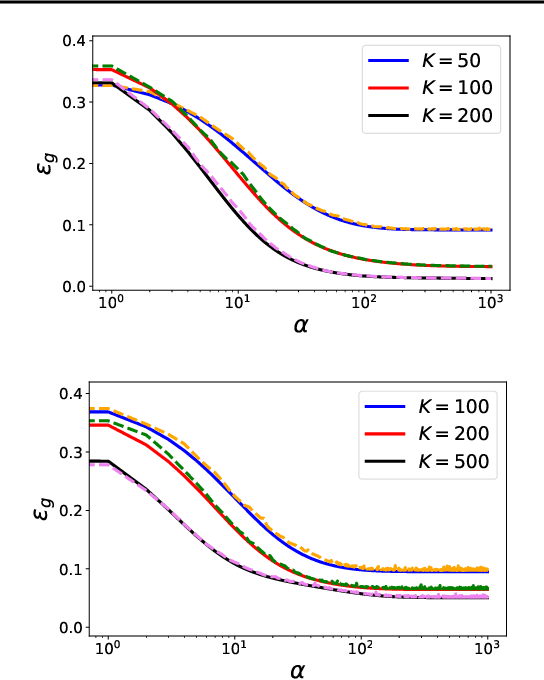
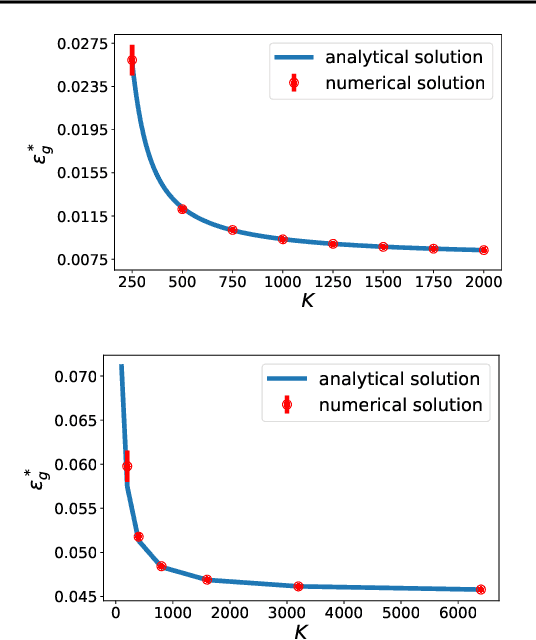
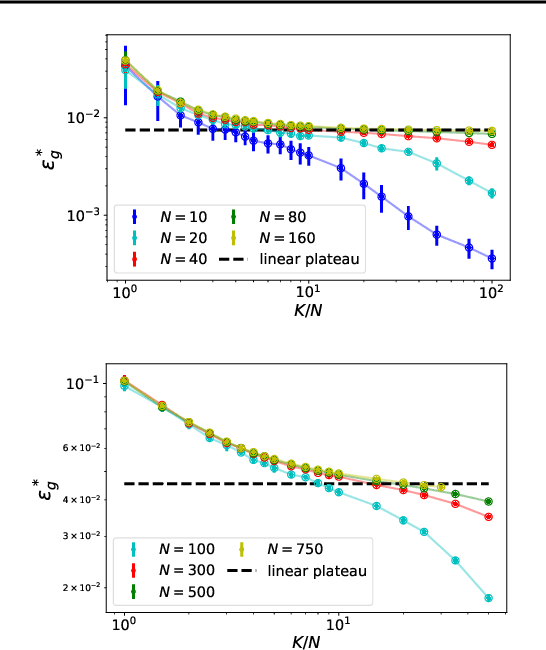
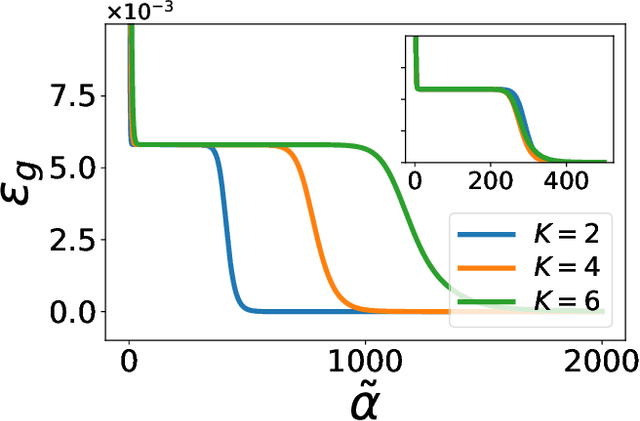
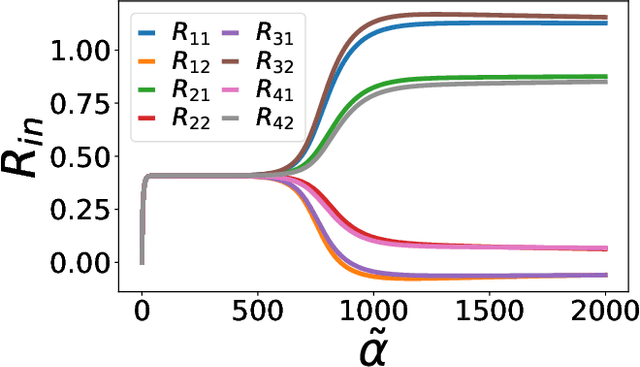
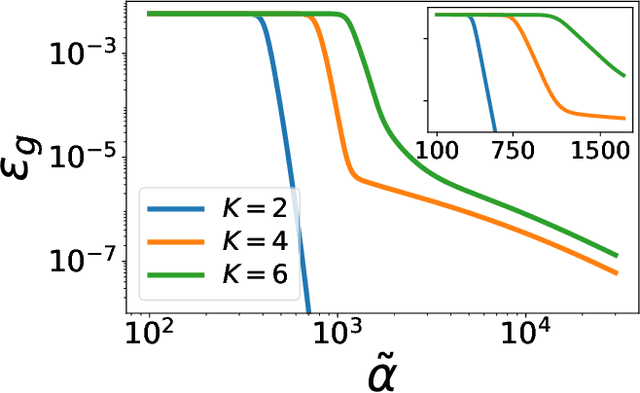
Neural scaling laws describe how the performance of deep neural networks scales with key factors such as training data size, model complexity, and training time, often following power-law behaviors over multiple orders of magnitude. Despite their empirical observation, the theoretical understanding of these scaling laws remains limited. In this work, we employ techniques from statistical mechanics to analyze one-pass stochastic gradient descent within a student-teacher framework, where both the student and teacher are two-layer neural networks. Our study primarily focuses on the generalization error and its behavior in response to data covariance matrices that exhibit power-law spectra. For linear activation functions, we derive analytical expressions for the generalization error, exploring different learning regimes and identifying conditions under which power-law scaling emerges. Additionally, we extend our analysis to non-linear activation functions in the feature learning regime, investigating how power-law spectra in the data covariance matrix impact learning dynamics. Importantly, we find that the length of the symmetric plateau depends on the number of distinct eigenvalues of the data covariance matrix and the number of hidden units, demonstrating how these plateaus behave under various configurations. In addition, our results reveal a transition from exponential to power-law convergence in the specialized phase when the data covariance matrix possesses a power-law spectrum. This work contributes to the theoretical understanding of neural scaling laws and provides insights into optimizing learning performance in practical scenarios involving complex data structures.

Online Learning for the Random Feature Model in the Student-Teacher Framework

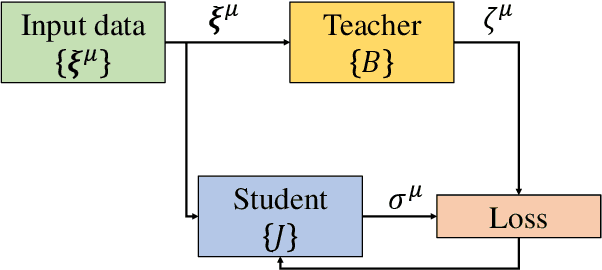
Deep neural networks are widely used prediction algorithms whose performance often improves as the number of weights increases, leading to over-parametrization. We consider a two-layered neural network whose first layer is frozen while the last layer is trainable, known as the random feature model. We study over-parametrization in the context of a student-teacher framework by deriving a set of differential equations for the learning dynamics. For any finite ratio of hidden layer size and input dimension, the student cannot generalize perfectly, and we compute the non-zero asymptotic generalization error. Only when the student's hidden layer size is exponentially larger than the input dimension, an approach to perfect generalization is possible.

Soft Mode in the Dynamics of Over-realizable On-line Learning for Soft Committee Machines

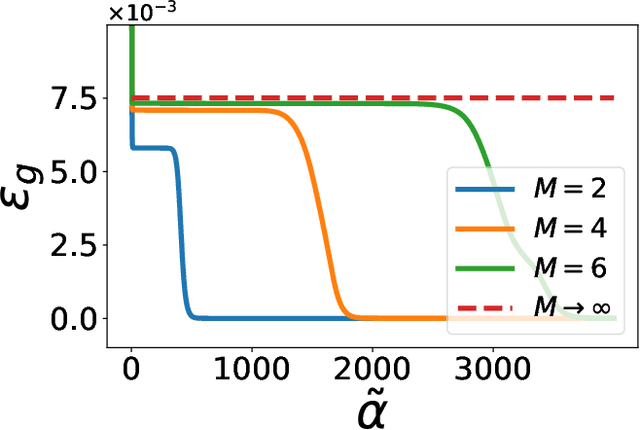
Over-parametrized deep neural networks trained by stochastic gradient descent are successful in performing many tasks of practical relevance. One aspect of over-parametrization is the possibility that the student network has a larger expressivity than the data generating process. In the context of a student-teacher scenario, this corresponds to the so-called over-realizable case, where the student network has a larger number of hidden units than the teacher. For on-line learning of a two-layer soft committee machine in the over-realizable case, we find that the approach to perfect learning occurs in a power-law fashion rather than exponentially as in the realizable case. All student nodes learn and replicate one of the teacher nodes if teacher and student outputs are suitably rescaled.