Statistical Precoder Design in Multi-User Systems via Graph Neural Networks and Generative Modeling

This letter proposes a graph neural network (GNN)-based framework for statistical precoder design that leverages model-based insights to compactly represent statistical knowledge, resulting in efficient, lightweight architectures. The framework also supports approximate statistical information in frequency division duplex (FDD) systems obtained through a Gaussian mixture model (GMM)-based limited feedback scheme in massive multiple-input multiple-output (MIMO) systems with low pilot overhead. Simulations using a spatial channel model and measurement data demonstrate the effectiveness of the proposed framework. It outperforms baseline methods, including stochastic iterative algorithms and Discrete Fourier transform (DFT) codebook-based approaches, particularly in low pilot overhead systems.

Decoupling Networks and Super-Quadratic Gains for RIS Systems with Mutual Coupling

We propose decoupling networks for the reconfigurable intelligent surface (RIS) array as a solution to benefit from the mutual coupling between the reflecting elements. In particular, we show that when incorporating these networks, the system model reduces to the same structure as if no mutual coupling is present. Hence, all algorithms and theoretical discussions neglecting mutual coupling can be directly applied when mutual coupling is present by utilizing our proposed decoupling networks. For example, by including decoupling networks, the channel gain maximization in RIS-aided single-input single-output (SISO) systems does not require an iterative algorithm but is given in closed form as opposed to using no decoupling network. In addition, this closed-form solution allows to analytically analyze scenarios under mutual coupling resulting in novel connections to the conventional transmit array gain. In particular, we show that super-quadratic (up to quartic) channel gains w.r.t. the number of RIS elements are possible and, therefore, the system with mutual coupling performs significantly better than the conventional uncoupled system in which only squared gains are possible. We consider diagonal as well as beyond diagonal (BD)-RISs and give various analytical and numerical results, including the inevitable losses at the RIS array. In addition, simulation results validate the superior performance of decoupling networks w.r.t. the channel gain compared to other state-of-the-art methods.

Sparse Bayesian Generative Modeling for Compressive Sensing

This work addresses the fundamental linear inverse problem in compressive sensing (CS) by introducing a new type of regularizing generative prior. Our proposed method utilizes ideas from classical dictionary-based CS and, in particular, sparse Bayesian learning (SBL), to integrate a strong regularization towards sparse solutions. At the same time, by leveraging the notion of conditional Gaussianity, it also incorporates the adaptability from generative models to training data. However, unlike most state-of-the-art generative models, it is able to learn from a few compressed and noisy data samples and requires no optimization algorithm for solving the inverse problem. Additionally, similar to Dirichlet prior networks, our model parameterizes a conjugate prior enabling its application for uncertainty quantification. We support our approach theoretically through the concept of variational inference and validate it empirically using different types of compressible signals.

A Versatile Pilot Design Scheme for FDD Systems Utilizing Gaussian Mixture Models

In this work, we propose a Gaussian mixture model (GMM)-based pilot design scheme for downlink (DL) channel estimation in single- and multi-user multiple-input multiple-output (MIMO) frequency division duplex (FDD) systems. In an initial offline phase, the GMM captures prior information during training, which is then utilized for pilot design. In the single-user case, the GMM is utilized to construct a codebook of pilot matrices and, once shared with the mobile terminal (MT), can be employed to determine a feedback index at the MT. This index selects a pilot matrix from the constructed codebook, eliminating the need for online pilot optimization. We further establish a sum conditional mutual information (CMI)-based pilot optimization framework for multi-user MIMO (MU-MIMO) systems. Based on the established framework, we utilize the GMM for pilot matrix design in MU-MIMO systems. The analytic representation of the GMM enables the adaptation to any signal-to-noise ratio (SNR) level and pilot configuration without re-training. Additionally, an adaption to any number of MTs is facilitated. Extensive simulations demonstrate the superior performance of the proposed pilot design scheme compared to state-of-the-art approaches. The performance gains can be exploited, e.g., to deploy systems with fewer pilots.

A Statistical Characterization of Wireless Channels Conditioned on Side Information

Statistical prior channel knowledge, such as the wide-sense-stationary-uncorrelated-scattering (WSSUS) property, and additional side information both can be used to enhance physical layer applications in wireless communication. Generally, the wireless channel's strongly fluctuating path phases and WSSUS property characterize the channel by a zero mean and Toeplitz-structured covariance matrices in different domains. In this work, we derive a framework to comprehensively categorize side information based on whether it preserves or abandons these statistical features conditioned on the given side information. To accomplish this, we combine insights from a generic channel model with the representation of wireless channels as probabilistic graphs. Additionally, we exemplify several applications, ranging from channel modeling to estimation and clustering, which demonstrate how the proposed framework can practically enhance physical layer methods utilizing machine learning (ML).

Channel-Adaptive Pilot Design for FDD-MIMO Systems Utilizing Gaussian Mixture Models

In this work, we propose to utilize Gaussian mixture models (GMMs) to design pilots for downlink (DL) channel estimation in frequency division duplex (FDD) systems. The GMM captures prior information during training that is leveraged to design a codebook of pilot matrices in an initial offline phase. Once shared with the mobile terminal (MT), the GMM is utilized to determine a feedback index at the MT in the online phase. This index selects a pilot matrix from a codebook, eliminating the need for online pilot optimization. The GMM is further used for DL channel estimation at the MT via observation-dependent linear minimum mean square error (LMMSE) filters, parametrized by the GMM. The analytic representation of the GMM allows adaptation to any signal-to-noise ratio (SNR) level and pilot configuration without re-training. With extensive simulations, we demonstrate the superior performance of the proposed GMM-based pilot scheme compared to state-of-the-art approaches.

On the Asymptotic Mean Square Error Optimality of Diffusion Probabilistic Models

Diffusion probabilistic models (DPMs) have recently shown great potential for denoising tasks. Despite their practical utility, there is a notable gap in their theoretical understanding. This paper contributes novel theoretical insights by rigorously proving the asymptotic convergence of a specific DPM denoising strategy to the mean square error (MSE)-optimal conditional mean estimator (CME) over a large number of diffusion steps. The studied DPM-based denoiser shares the training procedure of DPMs but distinguishes itself by forwarding only the conditional mean during the reverse inference process after training. We highlight the unique perspective that DPMs are composed of an asymptotically optimal denoiser while simultaneously inheriting a powerful generator by switching re-sampling in the reverse process on and off. The theoretical findings are validated by numerical results.

Wireless Channel Prediction via Gaussian Mixture Models

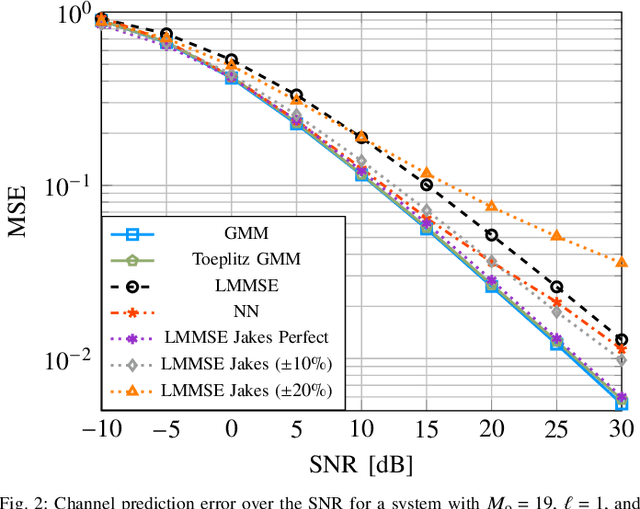
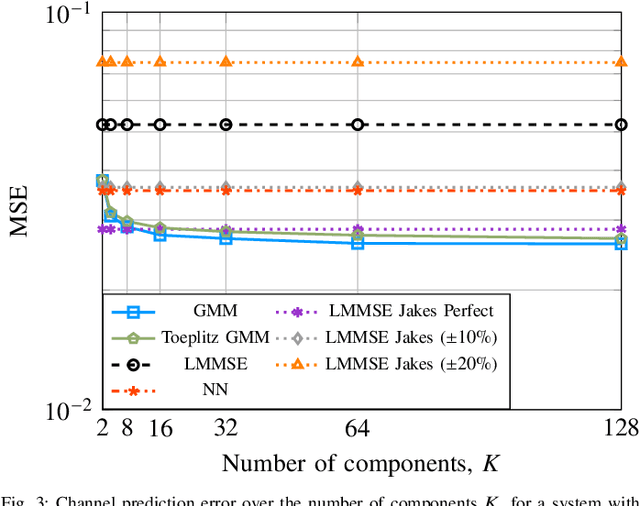
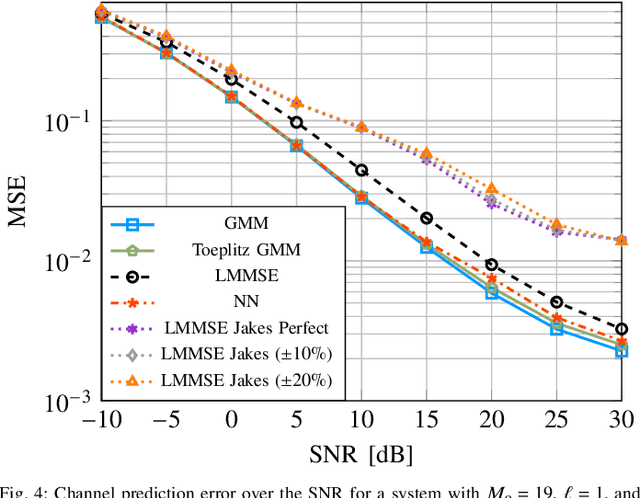
In this work, we utilize a Gaussian mixture model (GMM) to capture the underlying probability density function (PDF) of the channel trajectories of moving mobile terminals (MTs) within the coverage area of a base station (BS) in an offline phase. We propose to leverage the same GMM for channel prediction in the online phase. Our proposed approach does not require signal-to-noise ratio (SNR)-specific training and allows for parallelization. Numerical simulations for both synthetic and measured channel data demonstrate the effectiveness of our proposed GMM-based channel predictor compared to state-ofthe-art channel prediction methods.

Variational Autoencoder for Channel Estimation: Real-World Measurement Insights

This work utilizes a variational autoencoder for channel estimation and evaluates it on real-world measurements. The estimator is trained solely on noisy channel observations and parameterizes an approximation to the mean squared error-optimal estimator by learning observation-dependent conditional first and second moments. The proposed estimator significantly outperforms related state-of-the-art estimators on real-world measurements. We investigate the effect of pre-training with synthetic data and find that the proposed estimator exhibits comparable results to the related estimators if trained on synthetic data and evaluated on the measurement data. Furthermore, pre-training on synthetic data also helps to reduce the required measurement training dataset size.

Gohberg-Semencul Estimation of Toeplitz Structured Covariance Matrices and Their Inverses

When only few data samples are accessible, utilizing structural prior knowledge is essential for estimating covariance matrices and their inverses. One prominent example is knowing the covariance matrix to be Toeplitz structured, which occurs when dealing with wide sense stationary (WSS) processes. This work introduces a novel class of positive definiteness ensuring likelihood-based estimators for Toeplitz structured covariance matrices (CMs) and their inverses. In order to accomplish this, we derive positive definiteness enforcing constraint sets for the Gohberg-Semencul (GS) parameterization of inverse symmetric Toeplitz matrices. Motivated by the relationship between the GS parameterization and autoregressive (AR) processes, we propose hyperparameter tuning techniques, which enable our estimators to combine advantages from state-of-the-art likelihood and non-parametric estimators. Moreover, we present a computationally cheap closed-form estimator, which is derived by maximizing an approximate likelihood. Due to the ensured positive definiteness, our estimators perform well for both the estimation of the CM and the inverse covariance matrix (ICM). Extensive simulation results validate the proposed estimators' efficacy for several standard Toeplitz structured CMs commonly employed in a wide range of applications.