Neural Physicist: Learning Physical Dynamics from Image Sequences

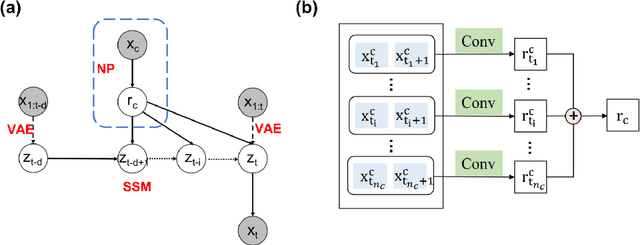
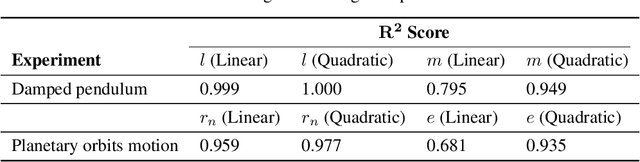
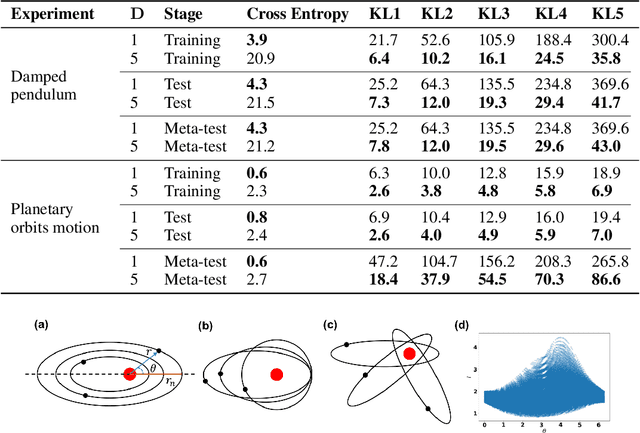
We present a novel architecture named Neural Physicist (NeurPhy) to learn physical dynamics directly from image sequences using deep neural networks. For any physical system, given the global system parameters, the time evolution of states is governed by the underlying physical laws. How to learn meaningful system representations in an end-to-end way and estimate accurate state transition dynamics facilitating long-term prediction have been long-standing challenges. In this paper, by leveraging recent progresses in representation learning and state space models (SSMs), we propose NeurPhy, which uses variational auto-encoder (VAE) to extract underlying Markovian dynamic state at each time step, neural process (NP) to extract the global system parameters, and a non-linear non-recurrent stochastic state space model to learn the physical dynamic transition. We apply NeurPhy to two physical experimental environments, i.e., damped pendulum and planetary orbits motion, and achieve promising results. Our model can not only extract the physically meaningful state representations, but also learn the state transition dynamics enabling long-term predictions for unseen image sequences. Furthermore, from the manifold dimension of the latent state space, we can easily identify the degree of freedom (DoF) of the underlying physical systems.

Riemannian Proximal Policy Optimization

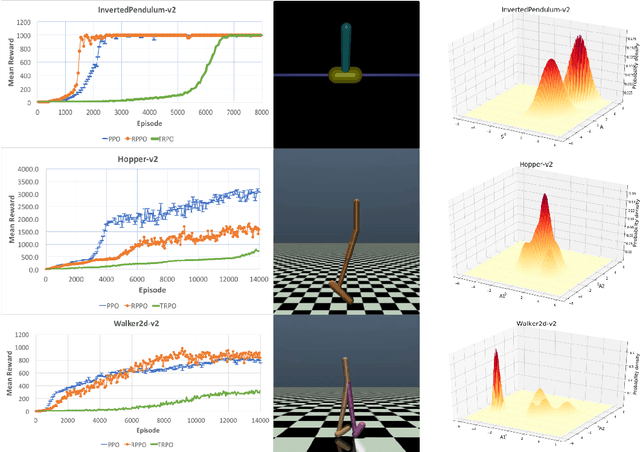
In this paper, We propose a general Riemannian proximal optimization algorithm with guaranteed convergence to solve Markov decision process (MDP) problems. To model policy functions in MDP, we employ Gaussian mixture model (GMM) and formulate it as a nonconvex optimization problem in the Riemannian space of positive semidefinite matrices. For two given policy functions, we also provide its lower bound on policy improvement by using bounds derived from the Wasserstein distance of GMMs. Preliminary experiments show the efficacy of our proposed Riemannian proximal policy optimization algorithm.

A Riemannian Primal-dual Algorithm Based on Proximal Operator and its Application in Metric Learning

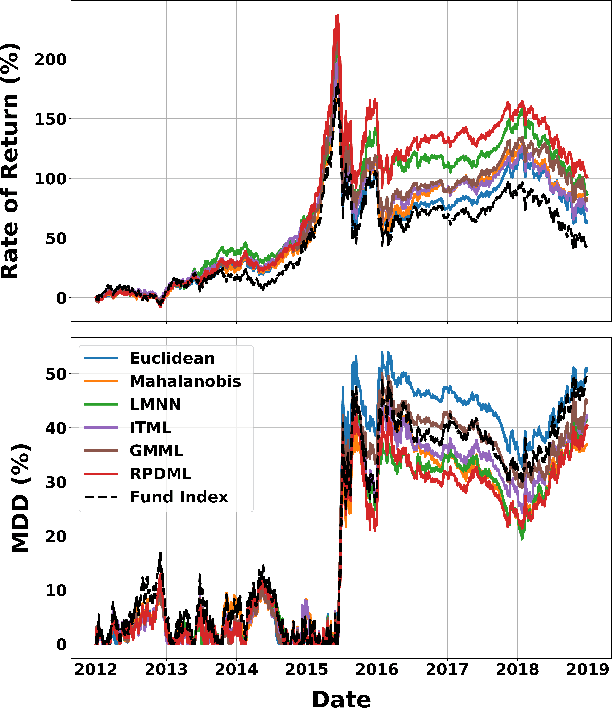
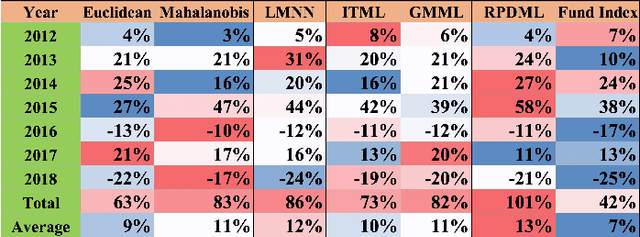
In this paper, we consider optimizing a smooth, convex, lower semicontinuous function in Riemannian space with constraints. To solve the problem, we first convert it to a dual problem and then propose a general primal-dual algorithm to optimize the primal and dual variables iteratively. In each optimization iteration, we employ a proximal operator to search optimal solution in the primal space. We prove convergence of the proposed algorithm and show its non-asymptotic convergence rate. By utilizing the proposed primal-dual optimization technique, we propose a novel metric learning algorithm which learns an optimal feature transformation matrix in the Riemannian space of positive definite matrices. Preliminary experimental results on an optimal fund selection problem in fund of funds (FOF) management for quantitative investment showed its efficacy.