A Riemannian Primal-dual Algorithm Based on Proximal Operator and its Application in Metric Learning
Paper and Code
May 19, 2020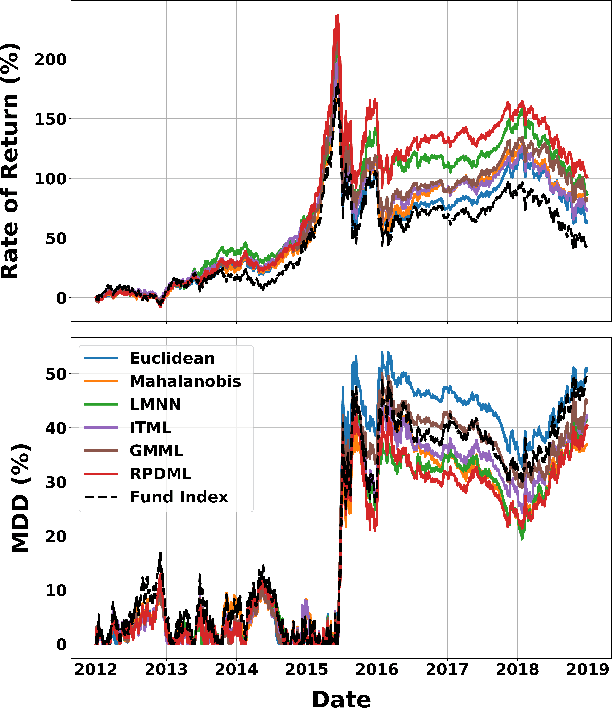
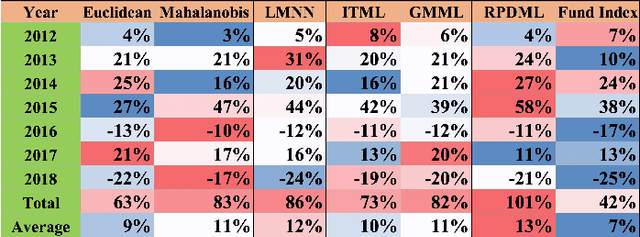
In this paper, we consider optimizing a smooth, convex, lower semicontinuous function in Riemannian space with constraints. To solve the problem, we first convert it to a dual problem and then propose a general primal-dual algorithm to optimize the primal and dual variables iteratively. In each optimization iteration, we employ a proximal operator to search optimal solution in the primal space. We prove convergence of the proposed algorithm and show its non-asymptotic convergence rate. By utilizing the proposed primal-dual optimization technique, we propose a novel metric learning algorithm which learns an optimal feature transformation matrix in the Riemannian space of positive definite matrices. Preliminary experimental results on an optimal fund selection problem in fund of funds (FOF) management for quantitative investment showed its efficacy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge