Eventprop training for efficient neuromorphic applications

Neuromorphic computing can reduce the energy requirements of neural networks and holds the promise to `repatriate' AI workloads back from the cloud to the edge. However, training neural networks on neuromorphic hardware has remained elusive. Here, we instead present a pipeline for training spiking neural networks on GPUs, using the efficient event-driven Eventprop algorithm implemented in mlGeNN, and deploying them on Intel's Loihi 2 neuromorphic chip. Our benchmarking on keyword spotting tasks indicates that there is almost no loss in accuracy between GPU and Loihi 2 implementations and that classifying a sample on Loihi 2 is up to 10X faster and uses 200X less energy than on an NVIDIA Jetson Orin Nano.

Efficient Event-based Delay Learning in Spiking Neural Networks

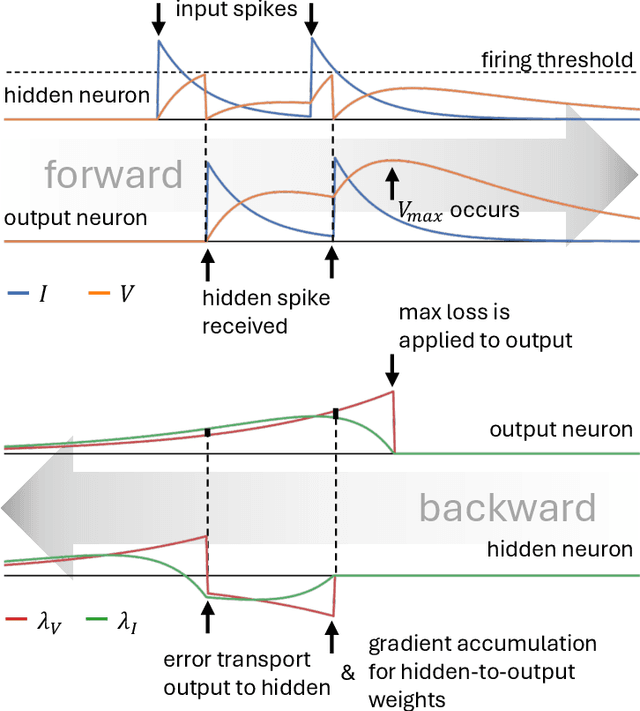
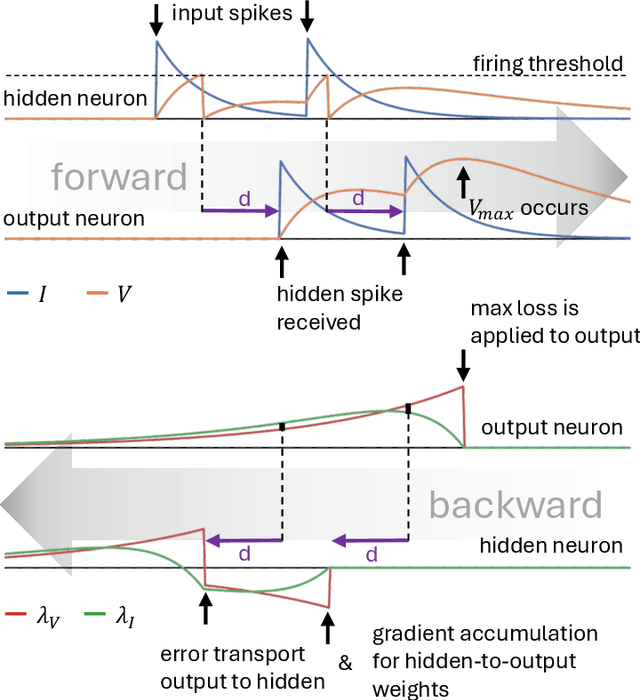
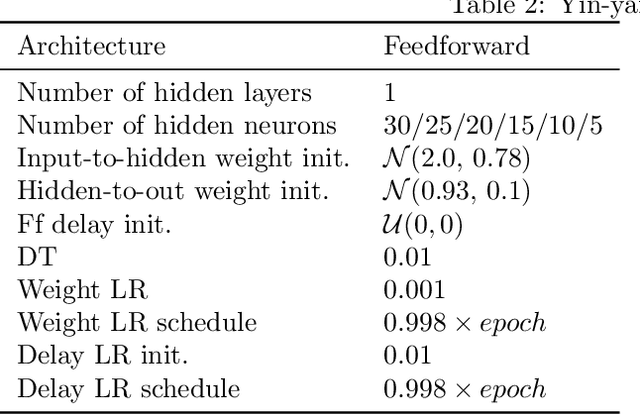
Spiking Neural Networks (SNNs) are attracting increased attention as a more energy-efficient alternative to traditional Artificial Neural Networks. Spiking neurons are stateful and intrinsically recurrent, making them well-suited for spatio-temporal tasks. However, this intrinsic memory is limited by synaptic and membrane time constants. A powerful additional mechanism are delays. In this paper, we propose a novel event-based training method for SNNs with delays, grounded in the EventProp formalism and enabling the calculation of exact gradients with respect to weights and delays. Our method supports multiple spikes per neuron and, to our best knowledge, is the first delay learning method applicable to recurrent connections. We evaluate our method on a simple sequence detection task, and the Yin-Yang, Spiking Heidelberg Digits and Spiking Speech Commands datasets, demonstrating that our algorithm can optimize delays from suboptimal initial conditions and enhance classification accuracy compared to architectures without delays. Finally, we show that our approach uses less than half the memory of the current state-of-the-art delay-learning method and is up to 26x faster.

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness

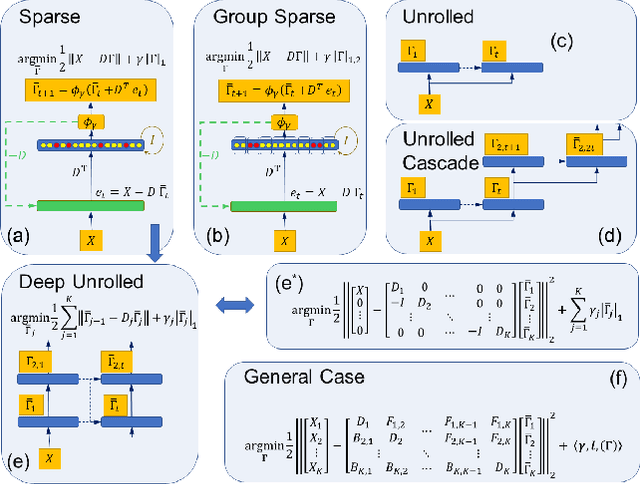
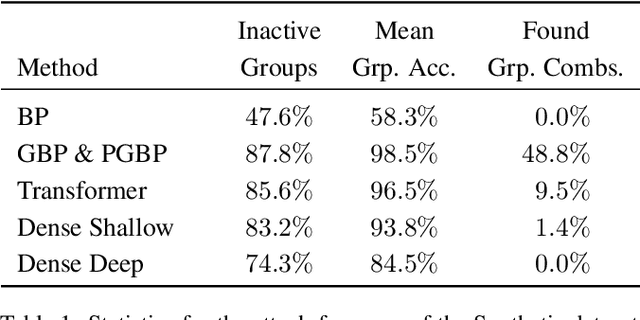
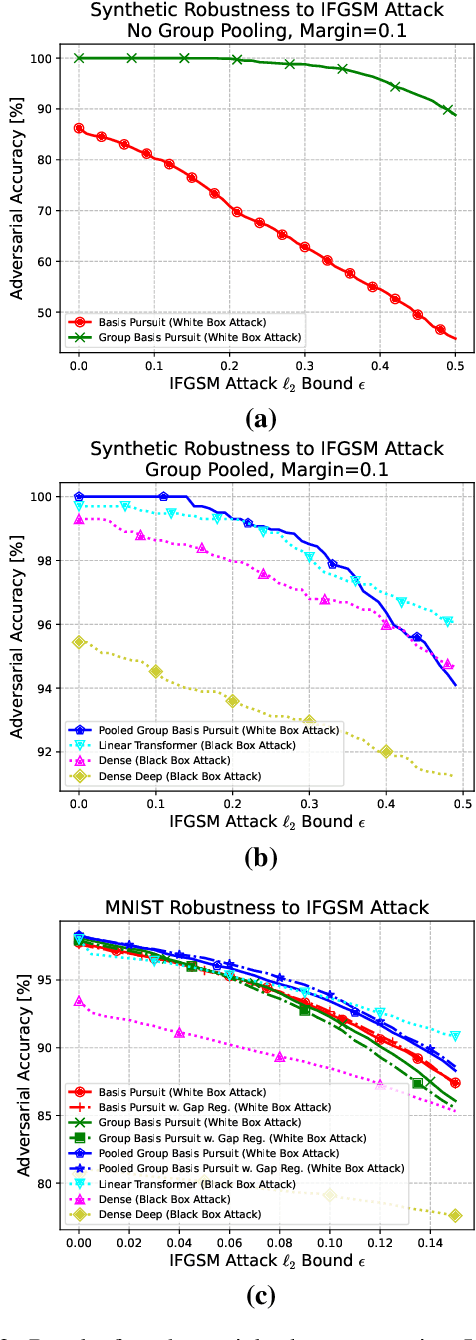
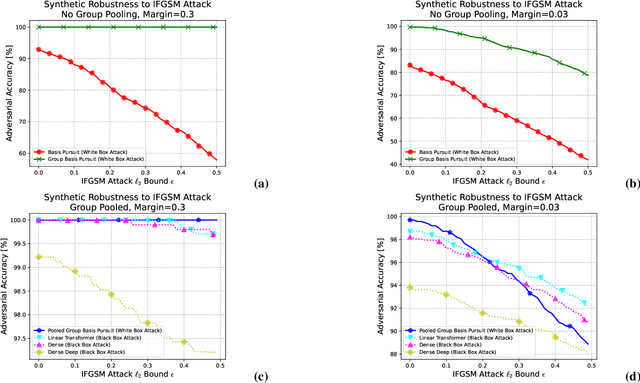
While deep neural networks are sensitive to adversarial noise, sparse coding using the Basis Pursuit (BP) method is robust against such attacks, including its multi-layer extensions. We prove that the stability theorem of BP holds upon the following generalizations: (i) the regularization procedure can be separated into disjoint groups with different weights, (ii) neurons or full layers may form groups, and (iii) the regularizer takes various generalized forms of the $\ell_1$ norm. This result provides the proof for the architectural generalizations of Cazenavette et al. (2021), including (iv) an approximation of the complete architecture as a shallow sparse coding network. Due to this approximation, we settled to experimenting with shallow networks and studied their robustness against the Iterative Fast Gradient Sign Method on a synthetic dataset and MNIST. We introduce classification based on the $\ell_2$ norms of the groups and show numerically that it can be accurate and offers considerable speedups. In this family, linear transformer shows the best performance. Based on the theoretical results and the numerical simulations, we highlight numerical matters that may improve performance further.