Multimodal Foundational Models for Unsupervised 3D General Obstacle Detection

Current autonomous driving perception models primarily rely on supervised learning with predefined categories. However, these models struggle to detect general obstacles not included in the fixed category set due to their variability and numerous edge cases. To address this issue, we propose a combination of multimodal foundational model-based obstacle segmentation with traditional unsupervised computational geometry-based outlier detection. Our approach operates offline, allowing us to leverage non-causality, and utilizes training-free methods. This enables the detection of general obstacles in 3D without the need for expensive retraining. To overcome the limitations of publicly available obstacle detection datasets, we collected and annotated our dataset, which includes various obstacles even in distant regions.

aiMotive Dataset: A Multimodal Dataset for Robust Autonomous Driving with Long-Range Perception

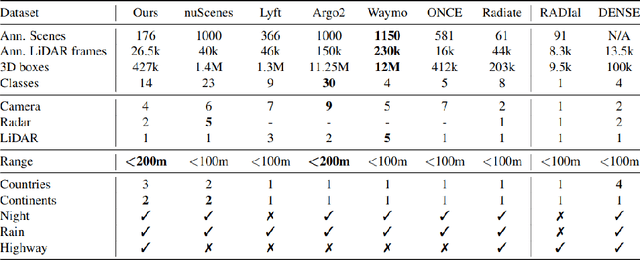
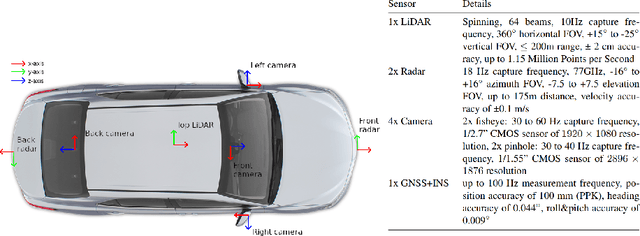
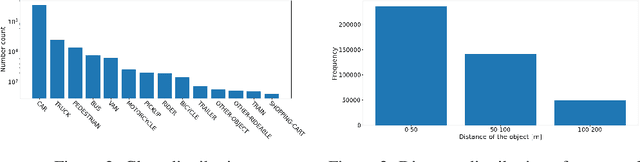
Autonomous driving is a popular research area within the computer vision research community. Since autonomous vehicles are highly safety-critical, ensuring robustness is essential for real-world deployment. While several public multimodal datasets are accessible, they mainly comprise two sensor modalities (camera, LiDAR) which are not well suited for adverse weather. In addition, they lack far-range annotations, making it harder to train neural networks that are the base of a highway assistant function of an autonomous vehicle. Therefore, we introduce a multimodal dataset for robust autonomous driving with long-range perception. The dataset consists of 176 scenes with synchronized and calibrated LiDAR, camera, and radar sensors covering a 360-degree field of view. The collected data was captured in highway, urban, and suburban areas during daytime, night, and rain and is annotated with 3D bounding boxes with consistent identifiers across frames. Furthermore, we trained unimodal and multimodal baseline models for 3D object detection. Data are available at \url{https://github.com/aimotive/aimotive_dataset}.

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness

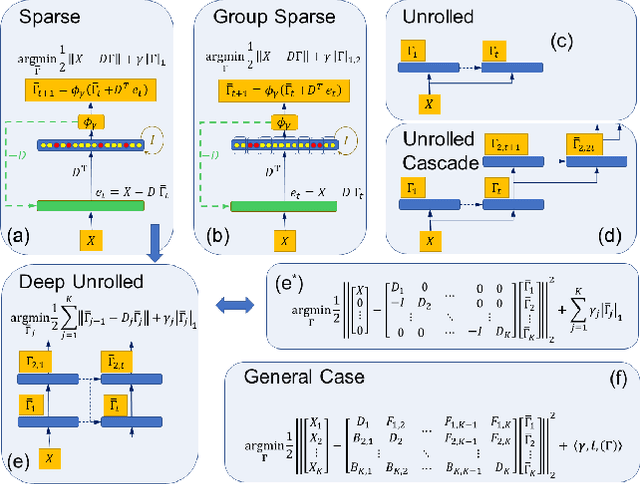
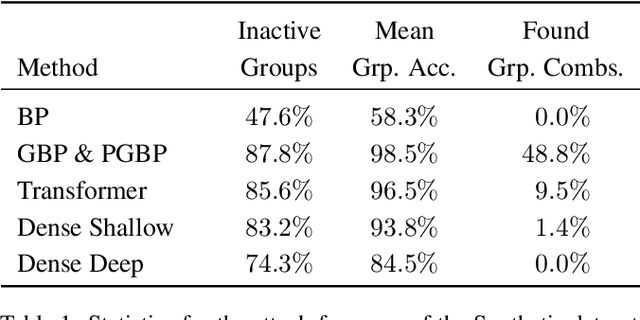
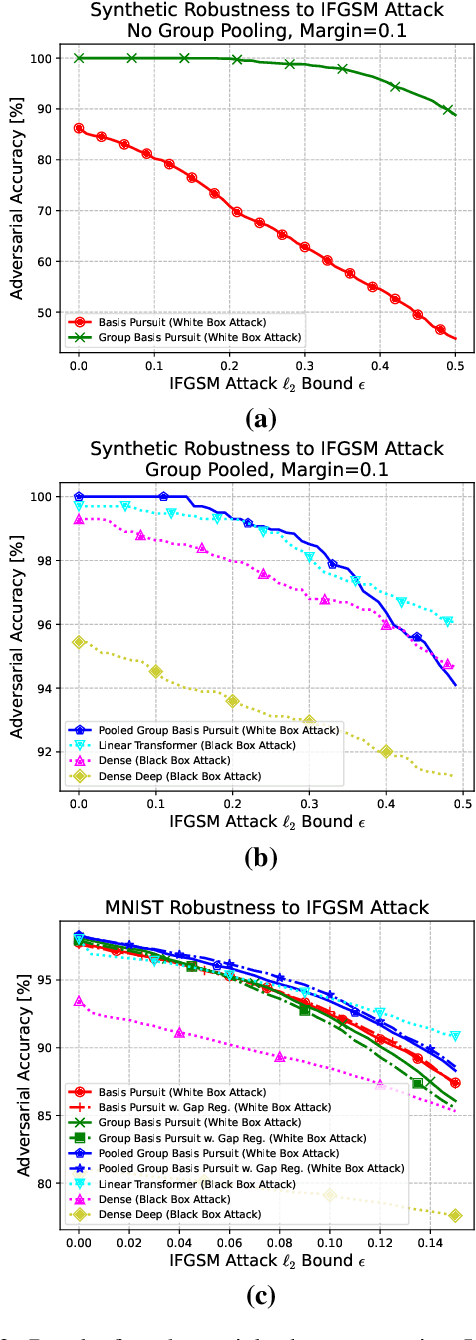
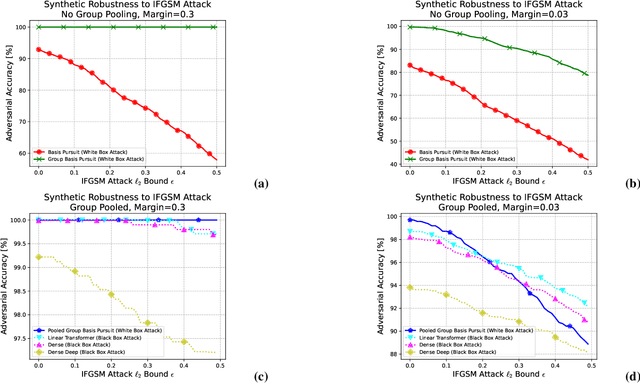
While deep neural networks are sensitive to adversarial noise, sparse coding using the Basis Pursuit (BP) method is robust against such attacks, including its multi-layer extensions. We prove that the stability theorem of BP holds upon the following generalizations: (i) the regularization procedure can be separated into disjoint groups with different weights, (ii) neurons or full layers may form groups, and (iii) the regularizer takes various generalized forms of the $\ell_1$ norm. This result provides the proof for the architectural generalizations of Cazenavette et al. (2021), including (iv) an approximation of the complete architecture as a shallow sparse coding network. Due to this approximation, we settled to experimenting with shallow networks and studied their robustness against the Iterative Fast Gradient Sign Method on a synthetic dataset and MNIST. We introduce classification based on the $\ell_2$ norms of the groups and show numerically that it can be accurate and offers considerable speedups. In this family, linear transformer shows the best performance. Based on the theoretical results and the numerical simulations, we highlight numerical matters that may improve performance further.