Ranking-based Argumentation Semantics Applied to Logical Argumentation (full version)

In formal argumentation, a distinction can be made between extension-based semantics, where sets of arguments are either (jointly) accepted or not, and ranking-based semantics, where grades of acceptability are assigned to arguments. Another important distinction is that between abstract approaches, that abstract away from the content of arguments, and structured approaches, that specify a method of constructing argument graphs on the basis of a knowledge base. While ranking-based semantics have been extensively applied to abstract argumentation, few work has been done on ranking-based semantics for structured argumentation. In this paper, we make a systematic investigation into the behaviour of ranking-based semantics applied to existing formalisms for structured argumentation. We show that a wide class of ranking-based semantics gives rise to so-called culpability measures, and are relatively robust to specific choices in argument construction methods.

Extracting Frequent Gradual Patterns Using Constraints Modeling

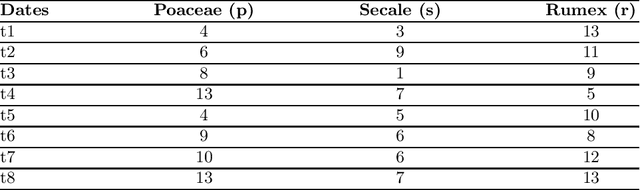
In this paper, we propose a constraint-based modeling approach for the problem of discovering frequent gradual patterns in a numerical dataset. This SAT-based declarative approach offers an additional possibility to benefit from the recent progress in satisfiability testing and to exploit the efficiency of modern SAT solvers for enumerating all frequent gradual patterns in a numerical dataset. Our approach can easily be extended with extra constraints, such as temporal constraints in order to extract more specific patterns in a broad range of gradual patterns mining applications. We show the practical feasibility of our SAT model by running experiments on two real world datasets.

Efficient Encodings of Conditional Cardinality Constraints

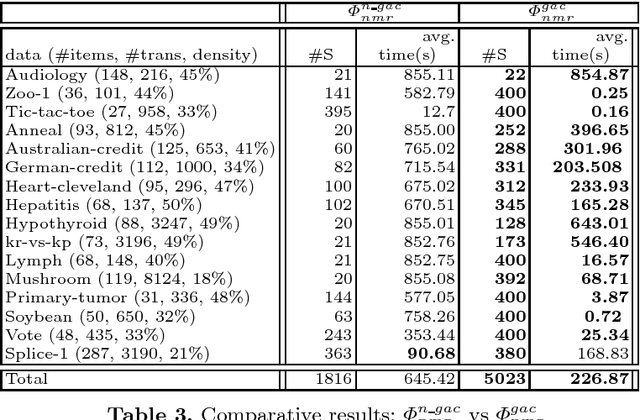
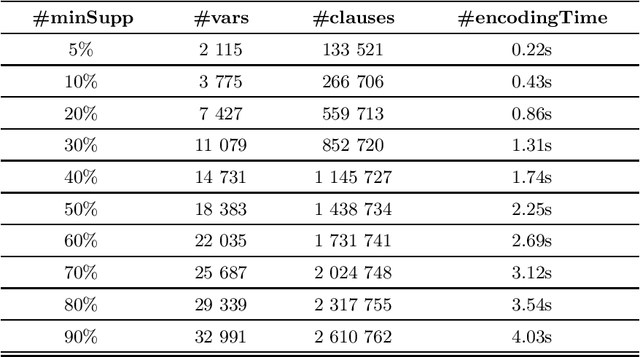
In the encoding of many real-world problems to propositional satisfiability, the cardinality constraint is a recurrent constraint that needs to be managed effectively. Several efficient encodings have been proposed while missing that such a constraint can be involved in a more general propositional formulation. To avoid combinatorial explosion, Tseitin principle usually used to translate such general propositional formula to Conjunctive Normal Form (CNF), introduces fresh propositional variables to represent sub-formulas and/or complex contraints. Thanks to Plaisted and Greenbaum improvement, the polarity of the sub-formula $\Phi$ is taken into account leading to conditional constraints of the form $y\rightarrow \Phi$, or $\Phi\rightarrow y$, where $y$ is a fresh propositional variable. In the case where $\Phi$ represents a cardinality constraint, such translation leads to conditional cardinality constraints subject of the present paper. We first show that when all the clauses encoding the cardinality constraint are augmented with an additional new variable, most of the well-known encodings cease to maintain the generalized arc consistency property. Then, we consider some of these encodings and show how they can be extended to recover such important property. An experimental validation is conducted on a SAT-based pattern mining application, where such conditional cardinality constraints is a cornerstone, showing the relevance of our proposed approach.

On the measure of conflicts: A MUS-Decomposition Based Framework

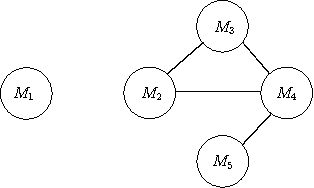
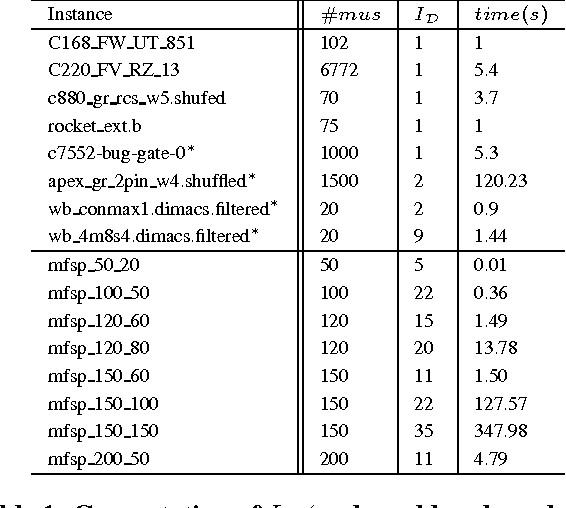
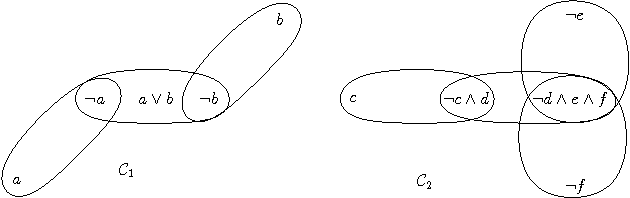
Measuring inconsistency is viewed as an important issue related to handling inconsistencies. Good measures are supposed to satisfy a set of rational properties. However, defining sound properties is sometimes problematic. In this paper, we emphasize one such property, named Decomposability, rarely discussed in the literature due to its modeling difficulties. To this end, we propose an independent decomposition which is more intuitive than existing proposals. To analyze inconsistency in a more fine-grained way, we introduce a graph representation of a knowledge base and various MUSdecompositions. One particular MUS-decomposition, named distributable MUS-decomposition leads to an interesting partition of inconsistencies in a knowledge base such that multiple experts can check inconsistencies in parallel, which is impossible under existing measures. Such particular MUSdecomposition results in an inconsistency measure that satisfies a number of desired properties. Moreover, we give an upper bound complexity of the measure that can be computed using 0/1 linear programming or Min Cost Satisfiability problems, and conduct preliminary experiments to show its feasibility.