Extracting Seasonal Gradual Patterns from Temporal Sequence Data Using Periodic Patterns Mining

Mining frequent episodes aims at recovering sequential patterns from temporal data sequences, which can then be used to predict the occurrence of related events in advance. On the other hand, gradual patterns that capture co-variation of complex attributes in the form of " when X increases/decreases, Y increases/decreases" play an important role in many real world applications where huge volumes of complex numerical data must be handled. Recently, these patterns have received attention from the data mining community exploring temporal data who proposed methods to automatically extract gradual patterns from temporal data. However, to the best of our knowledge, no method has been proposed to extract gradual patterns that regularly appear at identical time intervals in many sequences of temporal data, despite the fact that such patterns may add knowledge to certain applications, such as e-commerce. In this paper, we propose to extract co-variations of periodically repeating attributes from the sequences of temporal data that we call seasonal gradual patterns. For this purpose, we formulate the task of mining seasonal gradual patterns as the problem of mining periodic patterns in multiple sequences and then we exploit periodic pattern mining algorithms to extract seasonal gradual patterns. We discuss specific features of these patterns and propose an approach for their extraction based on mining periodic frequent patterns common to multiple sequences. We also propose a new anti-monotonous support definition associated to these seasonal gradual patterns. The illustrative results obtained from some real world data sets show that the proposed approach is efficient and that it can extract small sets of patterns by filtering numerous nonseasonal patterns to identify the seasonal ones.

Discovering Frequent Gradual Itemsets with Imprecise Data

The gradual patterns that model the complex co-variations of attributes of the form "The more/less X, The more/less Y" play a crucial role in many real world applications where the amount of numerical data to manage is important, this is the biological data. Recently, these types of patterns have caught the attention of the data mining community, where several methods have been defined to automatically extract and manage these patterns from different data models. However, these methods are often faced the problem of managing the quantity of mined patterns, and in many practical applications, the calculation of all these patterns can prove to be intractable for the user-defined frequency threshold and the lack of focus leads to generating huge collections of patterns. Moreover another problem with the traditional approaches is that the concept of gradualness is defined just as an increase or a decrease. Indeed, a gradualness is considered as soon as the values of the attribute on both objects are different. As a result, numerous quantities of patterns extracted by traditional algorithms can be presented to the user although their gradualness is only a noise effect in the data. To address this issue, this paper suggests to introduce the gradualness thresholds from which to consider an increase or a decrease. In contrast to literature approaches, the proposed approach takes into account the distribution of attribute values, as well as the user's preferences on the gradualness threshold and makes it possible to extract gradual patterns on certain databases where literature approaches fail due to too large search space. Moreover, results from an experimental evaluation on real databases show that the proposed algorithm is scalable, efficient, and can eliminate numerous patterns that do not verify specific gradualness requirements to show a small set of patterns to the user.

Extracting Frequent Gradual Patterns Using Constraints Modeling

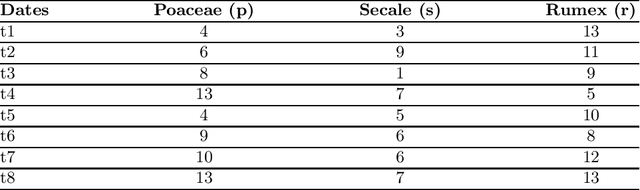
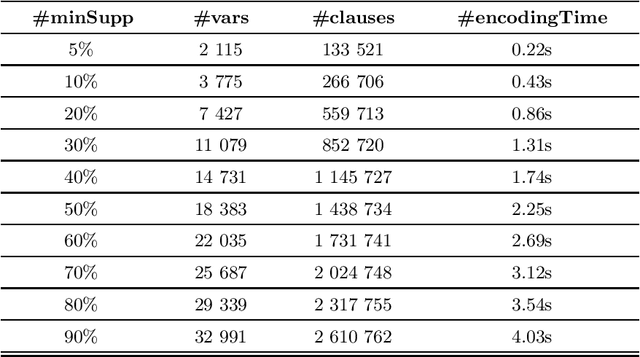
In this paper, we propose a constraint-based modeling approach for the problem of discovering frequent gradual patterns in a numerical dataset. This SAT-based declarative approach offers an additional possibility to benefit from the recent progress in satisfiability testing and to exploit the efficiency of modern SAT solvers for enumerating all frequent gradual patterns in a numerical dataset. Our approach can easily be extended with extra constraints, such as temporal constraints in order to extract more specific patterns in a broad range of gradual patterns mining applications. We show the practical feasibility of our SAT model by running experiments on two real world datasets.

Towards Learned Clauses Database Reduction Strategies Based on Dominance Relationship

Clause Learning is one of the most important components of a conflict driven clause learning (CDCL) SAT solver that is effective on industrial instances. Since the number of learned clauses is proved to be exponential in the worse case, it is necessary to identify the most relevant clauses to maintain and delete the irrelevant ones. As reported in the literature, several learned clauses deletion strategies have been proposed. However the diversity in both the number of clauses to be removed at each step of reduction and the results obtained with each strategy creates confusion to determine which criterion is better. Thus, the problem to select which learned clauses are to be removed during the search step remains very challenging. In this paper, we propose a novel approach to identify the most relevant learned clauses without favoring or excluding any of the proposed measures, but by adopting the notion of dominance relationship among those measures. Our approach bypasses the problem of the diversity of results and reaches a compromise between the assessments of these measures. Furthermore, the proposed approach also avoids another non-trivial problem which is the amount of clauses to be deleted at each reduction of the learned clause database.

Revisiting the Learned Clauses Database Reduction Strategies

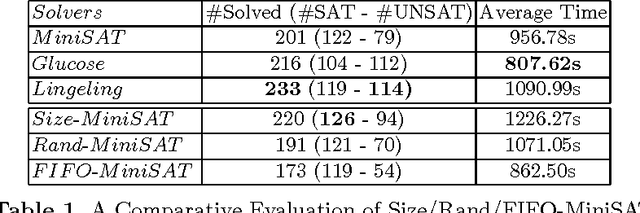
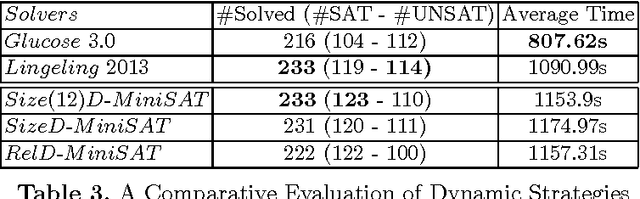
In this paper, we revisit an important issue of CDCL-based SAT solvers, namely the learned clauses database management policies. Our motivation takes its source from a simple observation on the remarkable performances of both random and size-bounded reduction strategies. We first derive a simple reduction strategy, called Size-Bounded Randomized strategy (in short SBR), that combines maintaing short clauses (of size bounded by k), while deleting randomly clauses of size greater than k. The resulting strategy outperform the state-of-the-art, namely the LBD based one, on SAT instances taken from the last SAT competition. Reinforced by the interest of keeping short clauses, we propose several new dynamic variants, and we discuss their performances.