Efficient Encodings of Conditional Cardinality Constraints

In the encoding of many real-world problems to propositional satisfiability, the cardinality constraint is a recurrent constraint that needs to be managed effectively. Several efficient encodings have been proposed while missing that such a constraint can be involved in a more general propositional formulation. To avoid combinatorial explosion, Tseitin principle usually used to translate such general propositional formula to Conjunctive Normal Form (CNF), introduces fresh propositional variables to represent sub-formulas and/or complex contraints. Thanks to Plaisted and Greenbaum improvement, the polarity of the sub-formula $\Phi$ is taken into account leading to conditional constraints of the form $y\rightarrow \Phi$, or $\Phi\rightarrow y$, where $y$ is a fresh propositional variable. In the case where $\Phi$ represents a cardinality constraint, such translation leads to conditional cardinality constraints subject of the present paper. We first show that when all the clauses encoding the cardinality constraint are augmented with an additional new variable, most of the well-known encodings cease to maintain the generalized arc consistency property. Then, we consider some of these encodings and show how they can be extended to recover such important property. An experimental validation is conducted on a SAT-based pattern mining application, where such conditional cardinality constraints is a cornerstone, showing the relevance of our proposed approach.

On SAT Models Enumeration in Itemset Mining

Frequent itemset mining is an essential part of data analysis and data mining. Recent works propose interesting SAT-based encodings for the problem of discovering frequent itemsets. Our aim in this work is to define strategies for adapting SAT solvers to such encodings in order to improve models enumeration. In this context, we deeply study the effects of restart, branching heuristics and clauses learning. We then conduct an experimental evaluation on SAT-Based itemset mining instances to show how SAT solvers can be adapted to obtain an efficient SAT model enumerator.

On the measure of conflicts: A MUS-Decomposition Based Framework

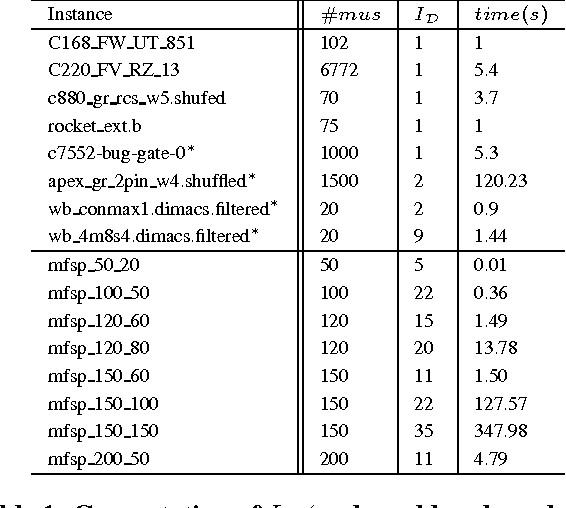
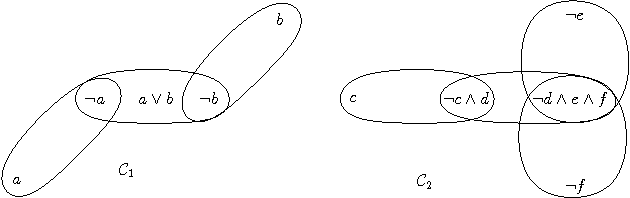
Measuring inconsistency is viewed as an important issue related to handling inconsistencies. Good measures are supposed to satisfy a set of rational properties. However, defining sound properties is sometimes problematic. In this paper, we emphasize one such property, named Decomposability, rarely discussed in the literature due to its modeling difficulties. To this end, we propose an independent decomposition which is more intuitive than existing proposals. To analyze inconsistency in a more fine-grained way, we introduce a graph representation of a knowledge base and various MUSdecompositions. One particular MUS-decomposition, named distributable MUS-decomposition leads to an interesting partition of inconsistencies in a knowledge base such that multiple experts can check inconsistencies in parallel, which is impossible under existing measures. Such particular MUSdecomposition results in an inconsistency measure that satisfies a number of desired properties. Moreover, we give an upper bound complexity of the measure that can be computed using 0/1 linear programming or Min Cost Satisfiability problems, and conduct preliminary experiments to show its feasibility.

Revisiting the Learned Clauses Database Reduction Strategies

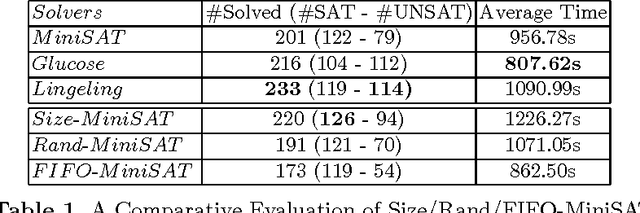
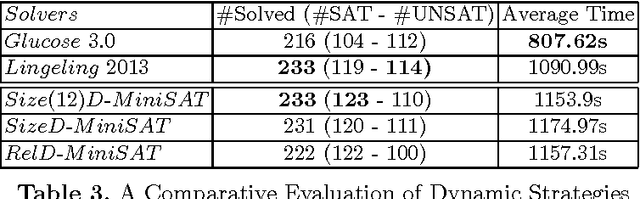
In this paper, we revisit an important issue of CDCL-based SAT solvers, namely the learned clauses database management policies. Our motivation takes its source from a simple observation on the remarkable performances of both random and size-bounded reduction strategies. We first derive a simple reduction strategy, called Size-Bounded Randomized strategy (in short SBR), that combines maintaing short clauses (of size bounded by k), while deleting randomly clauses of size greater than k. The resulting strategy outperform the state-of-the-art, namely the LBD based one, on SAT instances taken from the last SAT competition. Reinforced by the interest of keeping short clauses, we propose several new dynamic variants, and we discuss their performances.

A Mining-Based Compression Approach for Constraint Satisfaction Problems

In this paper, we propose an extension of our Mining for SAT framework to Constraint satisfaction Problem (CSP). We consider n-ary extensional constraints (table constraints). Our approach aims to reduce the size of the CSP by exploiting the structure of the constraints graph and of its associated microstructure. More precisely, we apply itemset mining techniques to search for closed frequent itemsets on these two representation. Using Tseitin extension, we rewrite the whole CSP to another compressed CSP equivalent with respect to satisfiability. Our approach contrast with previous proposed approach by Katsirelos and Walsh, as we do not change the structure of the constraints.

Extending Modern SAT Solvers for Enumerating All Models

In this paper, we address the problem of enumerating all models of a Boolean formula in conjunctive normal form (CNF). We propose an extension of CDCL-based SAT solvers to deal with this fundamental problem. Then, we provide an experimental evaluation of our proposed SAT model enumeration algorithms on both satisfiable SAT instances taken from the last SAT challenge and on instances from the SAT-based encoding of sequence mining problems.

Mining to Compact CNF Propositional Formulae

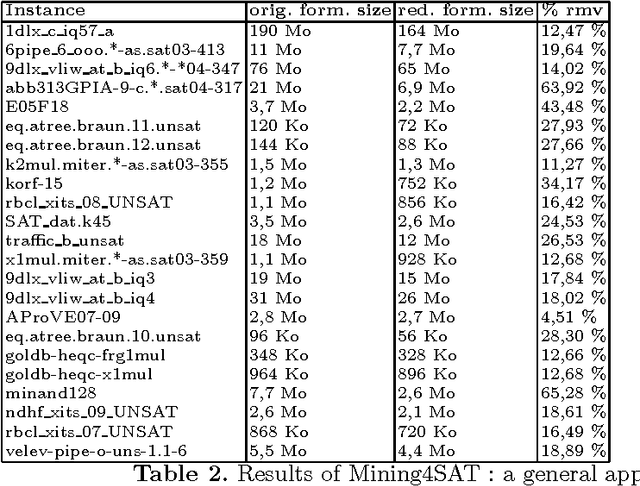
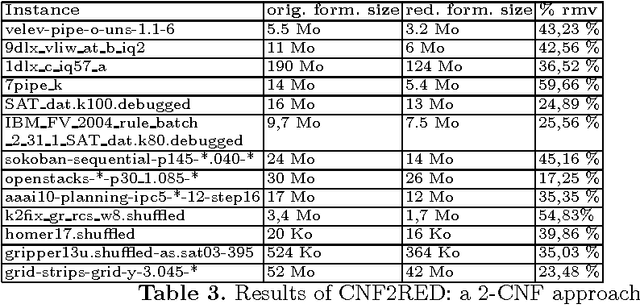
In this paper, we propose a first application of data mining techniques to propositional satisfiability. Our proposed Mining4SAT approach aims to discover and to exploit hidden structural knowledge for reducing the size of propositional formulae in conjunctive normal form (CNF). Mining4SAT combines both frequent itemset mining techniques and Tseitin's encoding for a compact representation of CNF formulae. The experiments of our Mining4SAT approach show interesting reductions of the sizes of many application instances taken from the last SAT competitions.

Learning for Dynamic subsumption

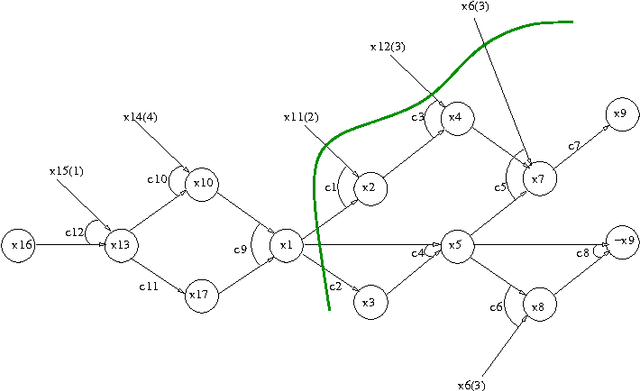
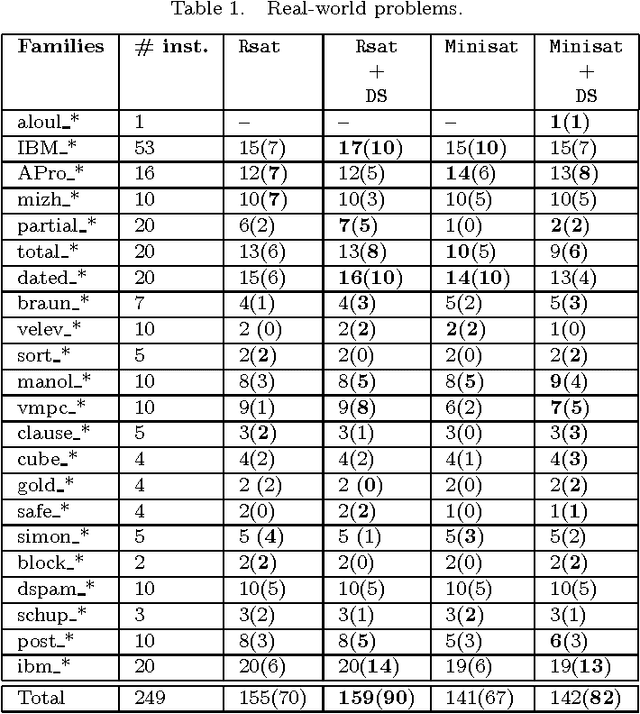
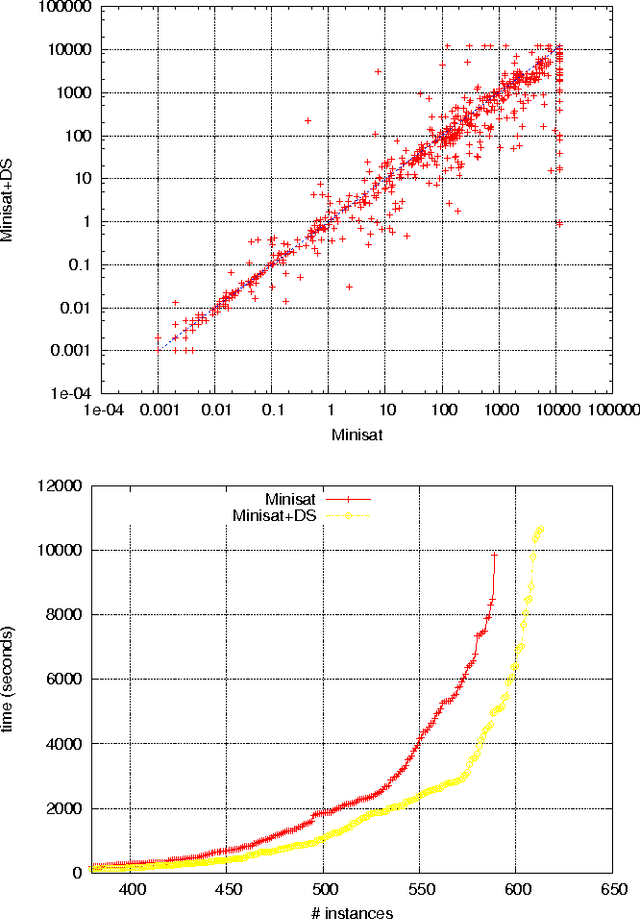
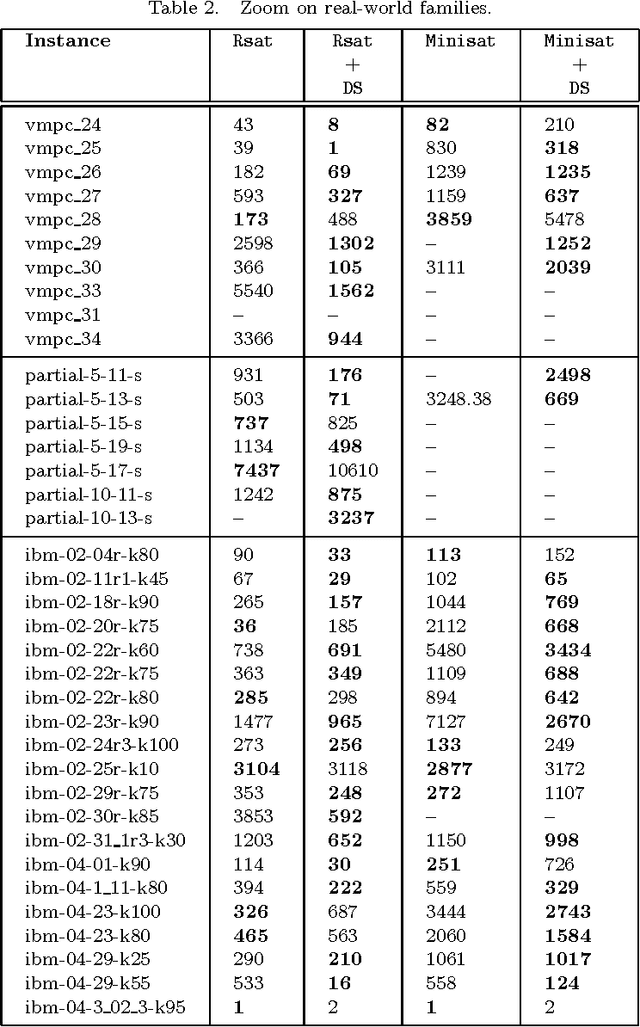
In this paper a new dynamic subsumption technique for Boolean CNF formulae is proposed. It exploits simple and sufficient conditions to detect during conflict analysis, clauses from the original formula that can be reduced by subsumption. During the learnt clause derivation, and at each step of the resolution process, we simply check for backward subsumption between the current resolvent and clauses from the original formula and encoded in the implication graph. Our approach give rise to a strong and dynamic simplification technique that exploits learning to eliminate literals from the original clauses. Experimental results show that the integration of our dynamic subsumption approach within the state-of-the-art SAT solvers Minisat and Rsat achieves interesting improvements particularly on crafted instances.