Length independent generalization bounds for deep SSM architectures with stability constraints

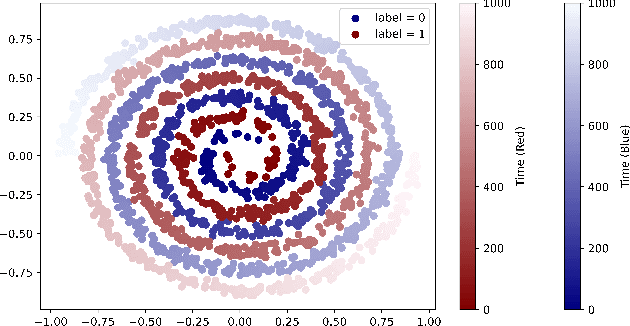
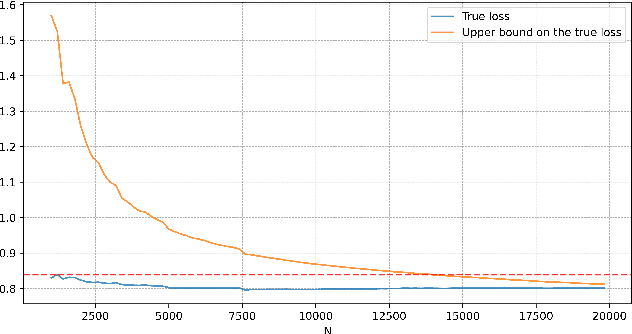
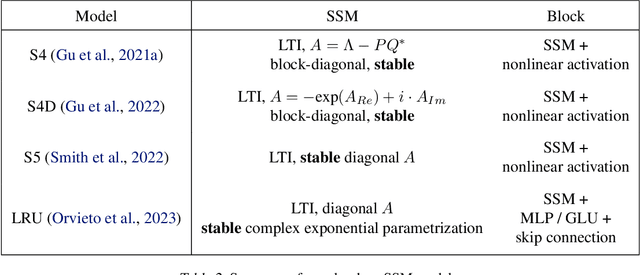
Many state-of-the-art models trained on long-range sequences, for example S4, S5 or LRU, are made of sequential blocks combining State-Space Models (SSMs) with neural networks. In this paper we provide a PAC bound that holds for these kind of architectures with stable SSM blocks and does not depend on the length of the input sequence. Imposing stability of the SSM blocks is a standard practice in the literature, and it is known to help performance. Our results provide a theoretical justification for the use of stable SSM blocks as the proposed PAC bound decreases as the degree of stability of the SSM blocks increases.

Optimization dependent generalization bound for ReLU networks based on sensitivity in the tangent bundle

Recent advances in deep learning have given us some very promising results on the generalization ability of deep neural networks, however literature still lacks a comprehensive theory explaining why heavily over-parametrized models are able to generalize well while fitting the training data. In this paper we propose a PAC type bound on the generalization error of feedforward ReLU networks via estimating the Rademacher complexity of the set of networks available from an initial parameter vector via gradient descent. The key idea is to bound the sensitivity of the network's gradient to perturbation of the input data along the optimization trajectory. The obtained bound does not explicitly depend on the depth of the network. Our results are experimentally verified on the MNIST and CIFAR-10 datasets.

PAC bounds of continuous Linear Parameter-Varying systems related to neural ODEs

We consider the problem of learning Neural Ordinary Differential Equations (neural ODEs) within the context of Linear Parameter-Varying (LPV) systems in continuous-time. LPV systems contain bilinear systems which are known to be universal approximators for non-linear systems. Moreover, a large class of neural ODEs can be embedded into LPV systems. As our main contribution we provide Probably Approximately Correct (PAC) bounds under stability for LPV systems related to neural ODEs. The resulting bounds have the advantage that they do not depend on the integration interval.

Gradient representations in ReLU networks as similarity functions

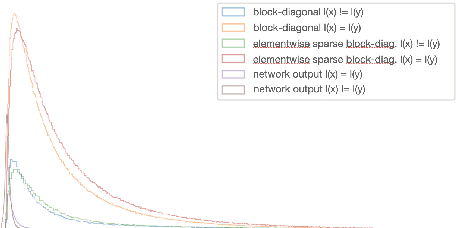
Feed-forward networks can be interpreted as mappings with linear decision surfaces at the level of the last layer. We investigate how the tangent space of the network can be exploited to refine the decision in case of ReLU (Rectified Linear Unit) activations. We show that a simple Riemannian metric parametrized on the parameters of the network forms a similarity function at least as good as the original network and we suggest a sparse metric to increase the similarity gap.

Quantum Inspired Adaptive Boosting

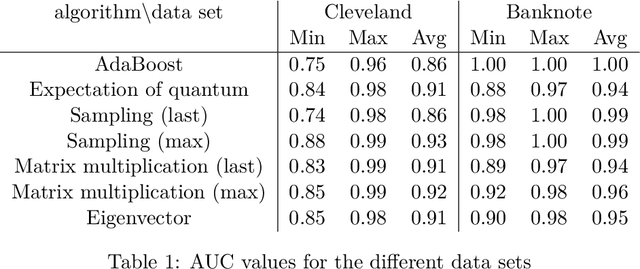
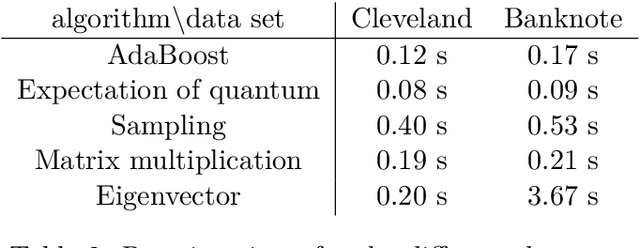
Building on the quantum ensemble based classifier algorithm of Schuld and Petruccione [arXiv:1704.02146v1], we devise equivalent classical algorithms which show that this quantum ensemble method does not have advantage over classical algorithms. Essentially, we simplify their algorithm until it is intuitive to come up with an equivalent classical version. One of the classical algorithms is extremely simple and runs in constant time for each input to be classified. We further develop the idea and, as the main contribution of the paper, we propose methods inspired by combining the quantum ensemble method with adaptive boosting. The algorithms were tested and found to be comparable to the AdaBoost algorithm on publicly available data sets.

Tangent Space Sensitivity and Distribution of Linear Regions in ReLU Networks

Recent articles indicate that deep neural networks are efficient models for various learning problems. However they are often highly sensitive to various changes that cannot be detected by an independent observer. As our understanding of deep neural networks with traditional generalization bounds still remains incomplete, there are several measures which capture the behaviour of the model in case of small changes at a specific state. In this paper we consider adversarial stability in the tangent space and suggest tangent sensitivity in order to characterize stability. We focus on a particular kind of stability with respect to changes in parameters that are induced by individual examples without known labels. We derive several easily computable bounds and empirical measures for feed-forward fully connected ReLU (Rectified Linear Unit) networks and connect tangent sensitivity to the distribution of the activation regions in the input space realized by the network. Our experiments suggest that even simple bounds and measures are associated with the empirical generalization gap.

Tangent Space Separability in Feedforward Neural Networks

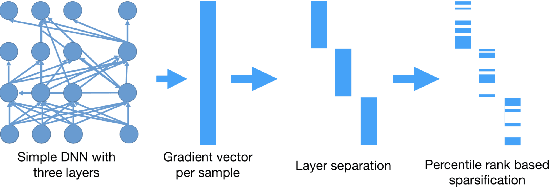
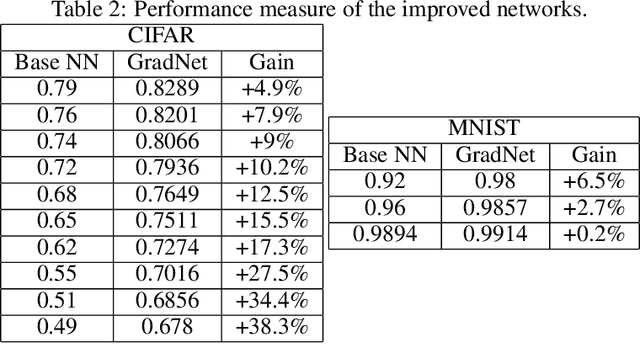
Hierarchical neural networks are exponentially more efficient than their corresponding "shallow" counterpart with the same expressive power, but involve huge number of parameters and require tedious amounts of training. By approximating the tangent subspace, we suggest a sparse representation that enables switching to shallow networks, GradNet after a very early training stage. Our experiments show that the proposed approximation of the metric improves and sometimes even surpasses the achievable performance of the original network significantly even after a few epochs of training the original feedforward network.

Expressive power of outer product manifolds on feed-forward neural networks

Hierarchical neural networks are exponentially more efficient than their corresponding "shallow" counterpart with the same expressive power, but involve huge number of parameters and require tedious amounts of training. Our main idea is to mathematically understand and describe the hierarchical structure of feedforward neural networks by reparametrization invariant Riemannian metrics. By computing or approximating the tangent subspace, we better utilize the original network via sparse representations that enables switching to shallow networks after a very early training stage. Our experiments show that the proposed approximation of the metric improves and sometimes even surpasses the achievable performance of the original network significantly even after a few epochs of training the original feedforward network.