Generalized Naive Bayes

In this paper we introduce the so-called Generalized Naive Bayes structure as an extension of the Naive Bayes structure. We give a new greedy algorithm that finds a good fitting Generalized Naive Bayes (GNB) probability distribution. We prove that this fits the data at least as well as the probability distribution determined by the classical Naive Bayes (NB). Then, under a not very restrictive condition, we give a second algorithm for which we can prove that it finds the optimal GNB probability distribution, i.e. best fitting structure in the sense of KL divergence. Both algorithms are constructed to maximize the information content and aim to minimize redundancy. Based on these algorithms, new methods for feature selection are introduced. We discuss the similarities and differences to other related algorithms in terms of structure, methodology, and complexity. Experimental results show, that the algorithms introduced outperform the related algorithms in many cases.

Tangent Space Separability in Feedforward Neural Networks

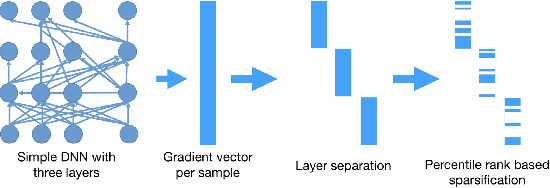
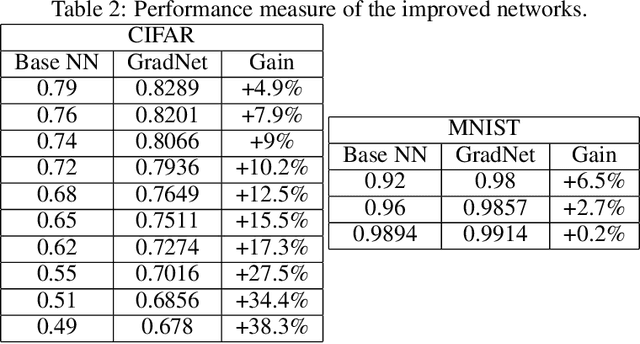
Hierarchical neural networks are exponentially more efficient than their corresponding "shallow" counterpart with the same expressive power, but involve huge number of parameters and require tedious amounts of training. By approximating the tangent subspace, we suggest a sparse representation that enables switching to shallow networks, GradNet after a very early training stage. Our experiments show that the proposed approximation of the metric improves and sometimes even surpasses the achievable performance of the original network significantly even after a few epochs of training the original feedforward network.

Expressive power of outer product manifolds on feed-forward neural networks

Hierarchical neural networks are exponentially more efficient than their corresponding "shallow" counterpart with the same expressive power, but involve huge number of parameters and require tedious amounts of training. Our main idea is to mathematically understand and describe the hierarchical structure of feedforward neural networks by reparametrization invariant Riemannian metrics. By computing or approximating the tangent subspace, we better utilize the original network via sparse representations that enables switching to shallow networks after a very early training stage. Our experiments show that the proposed approximation of the metric improves and sometimes even surpasses the achievable performance of the original network significantly even after a few epochs of training the original feedforward network.