Length independent generalization bounds for deep SSM architectures with stability constraints

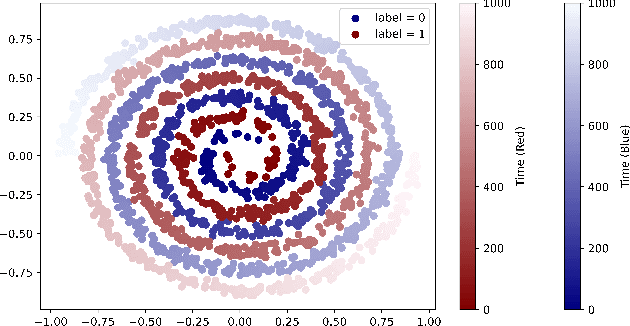
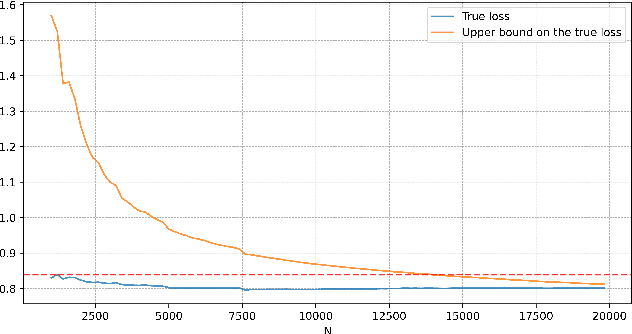
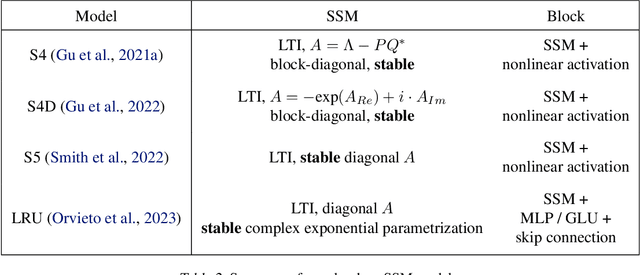
Many state-of-the-art models trained on long-range sequences, for example S4, S5 or LRU, are made of sequential blocks combining State-Space Models (SSMs) with neural networks. In this paper we provide a PAC bound that holds for these kind of architectures with stable SSM blocks and does not depend on the length of the input sequence. Imposing stability of the SSM blocks is a standard practice in the literature, and it is known to help performance. Our results provide a theoretical justification for the use of stable SSM blocks as the proposed PAC bound decreases as the degree of stability of the SSM blocks increases.

Optimization dependent generalization bound for ReLU networks based on sensitivity in the tangent bundle

Recent advances in deep learning have given us some very promising results on the generalization ability of deep neural networks, however literature still lacks a comprehensive theory explaining why heavily over-parametrized models are able to generalize well while fitting the training data. In this paper we propose a PAC type bound on the generalization error of feedforward ReLU networks via estimating the Rademacher complexity of the set of networks available from an initial parameter vector via gradient descent. The key idea is to bound the sensitivity of the network's gradient to perturbation of the input data along the optimization trajectory. The obtained bound does not explicitly depend on the depth of the network. Our results are experimentally verified on the MNIST and CIFAR-10 datasets.

Theoretical Evaluation of Asymmetric Shapley Values for Root-Cause Analysis

In this work, we examine Asymmetric Shapley Values (ASV), a variant of the popular SHAP additive local explanation method. ASV proposes a way to improve model explanations incorporating known causal relations between variables, and is also considered as a way to test for unfair discrimination in model predictions. Unexplored in previous literature, relaxing symmetry in Shapley values can have counter-intuitive consequences for model explanation. To better understand the method, we first show how local contributions correspond to global contributions of variance reduction. Using variance, we demonstrate multiple cases where ASV yields counter-intuitive attributions, arguably producing incorrect results for root-cause analysis. Second, we identify generalized additive models (GAM) as a restricted class for which ASV exhibits desirable properties. We support our arguments by proving multiple theoretical results about the method. Finally, we demonstrate the use of asymmetric attributions on multiple real-world datasets, comparing the results with and without restricted model families using gradient boosting and deep learning models.

PAC bounds of continuous Linear Parameter-Varying systems related to neural ODEs

We consider the problem of learning Neural Ordinary Differential Equations (neural ODEs) within the context of Linear Parameter-Varying (LPV) systems in continuous-time. LPV systems contain bilinear systems which are known to be universal approximators for non-linear systems. Moreover, a large class of neural ODEs can be embedded into LPV systems. As our main contribution we provide Probably Approximately Correct (PAC) bounds under stability for LPV systems related to neural ODEs. The resulting bounds have the advantage that they do not depend on the integration interval.