Gradient representations in ReLU networks as similarity functions
Paper and Code
Oct 26, 2021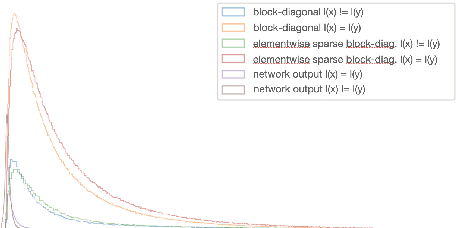
Feed-forward networks can be interpreted as mappings with linear decision surfaces at the level of the last layer. We investigate how the tangent space of the network can be exploited to refine the decision in case of ReLU (Rectified Linear Unit) activations. We show that a simple Riemannian metric parametrized on the parameters of the network forms a similarity function at least as good as the original network and we suggest a sparse metric to increase the similarity gap.
* Accepted at 29th ESANN 2021, 6-8 October 2021, Belgium, 7 pages, 1
figure
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge