A Revision of Neural Tangent Kernel-based Approaches for Neural Networks

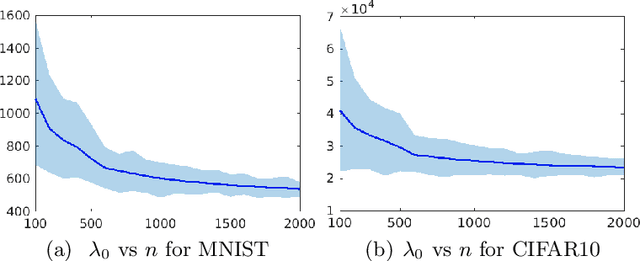
Recent theoretical works based on the neural tangent kernel (NTK) have shed light on the optimization and generalization of over-parameterized networks, and partially bridge the gap between their practical success and classical learning theory. Especially, using the NTK-based approach, the following three representative results were obtained: (1) A training error bound was derived to show that networks can fit any finite training sample perfectly by reflecting a tighter characterization of training speed depending on the data complexity. (2) A generalization error bound invariant of network size was derived by using a data-dependent complexity measure (CMD). It follows from this CMD bound that networks can generalize arbitrary smooth functions. (3) A simple and analytic kernel function was derived as indeed equivalent to a fully-trained network. This kernel outperforms its corresponding network and the existing gold standard, Random Forests, in few shot learning. For all of these results to hold, the network scaling factor $\kappa$ should decrease w.r.t. sample size n. In this case of decreasing $\kappa$, however, we prove that the aforementioned results are surprisingly erroneous. It is because the output value of trained network decreases to zero when $\kappa$ decreases w.r.t. n. To solve this problem, we tighten key bounds by essentially removing $\kappa$-affected values. Our tighter analysis resolves the scaling problem and enables the validation of the original NTK-based results.

Multitask Learning using Task Clustering with Applications to Predictive Modeling and GWAS of Plant Varieties

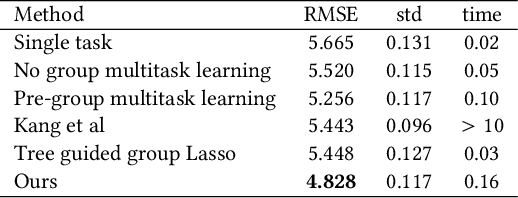
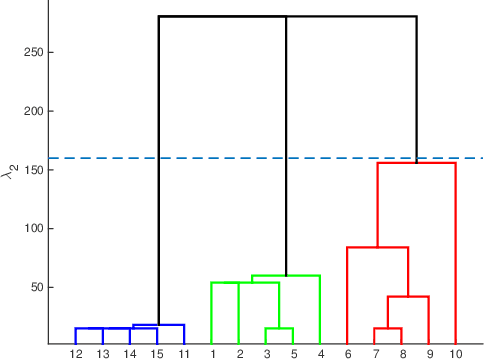
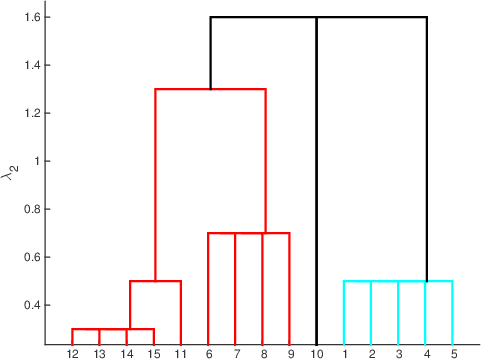
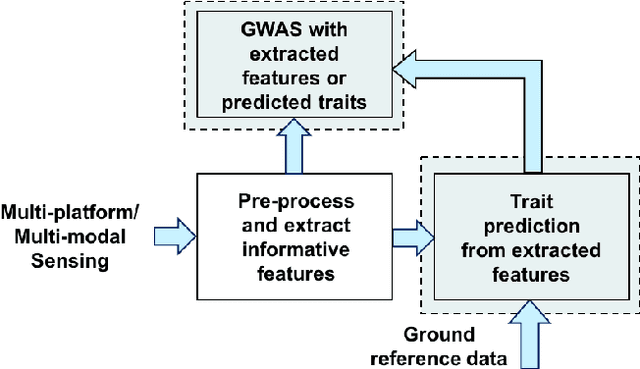
Inferring predictive maps between multiple input and multiple output variables or tasks has innumerable applications in data science. Multi-task learning attempts to learn the maps to several output tasks simultaneously with information sharing between them. We propose a novel multi-task learning framework for sparse linear regression, where a full task hierarchy is automatically inferred from the data, with the assumption that the task parameters follow a hierarchical tree structure. The leaves of the tree are the parameters for individual tasks, and the root is the global model that approximates all the tasks. We apply the proposed approach to develop and evaluate: (a) predictive models of plant traits using large-scale and automated remote sensing data, and (b) GWAS methodologies mapping such derived phenotypes in lieu of hand-measured traits. We demonstrate the superior performance of our approach compared to other methods, as well as the usefulness of discovering hierarchical groupings between tasks. Our results suggest that richer genetic mapping can indeed be obtained from the remote sensing data. In addition, our discovered groupings reveal interesting insights from a plant science perspective.

Learning task structure via sparsity grouped multitask learning

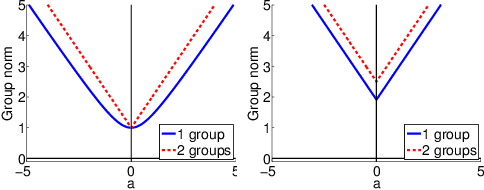
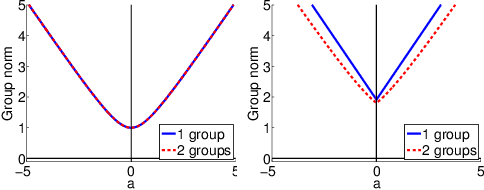
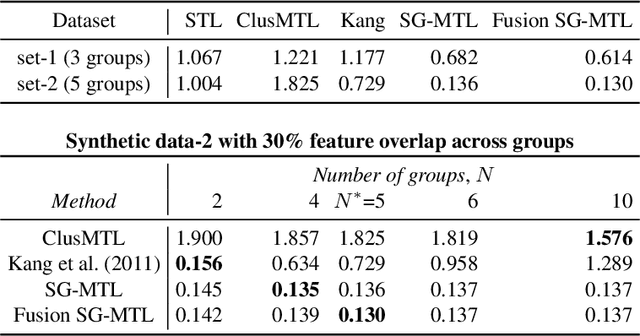
Sparse mapping has been a key methodology in many high-dimensional scientific problems. When multiple tasks share the set of relevant features, learning them jointly in a group drastically improves the quality of relevant feature selection. However, in practice this technique is used limitedly since such grouping information is usually hidden. In this paper, our goal is to recover the group structure on the sparsity patterns and leverage that information in the sparse learning. Toward this, we formulate a joint optimization problem in the task parameter and the group membership, by constructing an appropriate regularizer to encourage sparse learning as well as correct recovery of task groups. We further demonstrate that our proposed method recovers groups and the sparsity patterns in the task parameters accurately by extensive experiments.

Robust Gaussian Graphical Modeling with the Trimmed Graphical Lasso

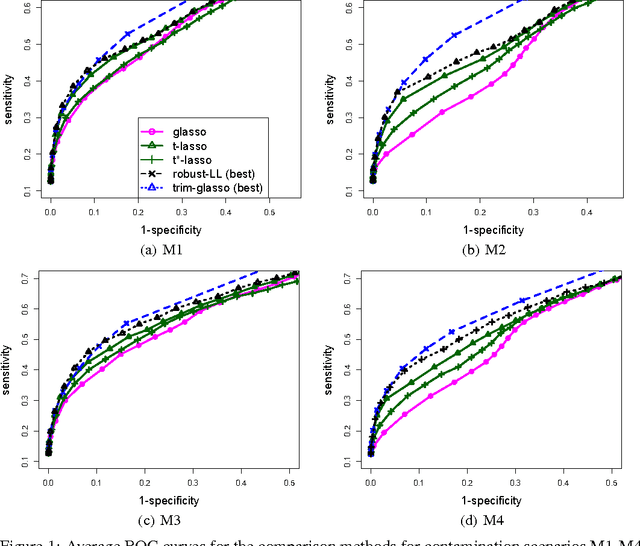
Gaussian Graphical Models (GGMs) are popular tools for studying network structures. However, many modern applications such as gene network discovery and social interactions analysis often involve high-dimensional noisy data with outliers or heavier tails than the Gaussian distribution. In this paper, we propose the Trimmed Graphical Lasso for robust estimation of sparse GGMs. Our method guards against outliers by an implicit trimming mechanism akin to the popular Least Trimmed Squares method used for linear regression. We provide a rigorous statistical analysis of our estimator in the high-dimensional setting. In contrast, existing approaches for robust sparse GGMs estimation lack statistical guarantees. Our theoretical results are complemented by experiments on simulated and real gene expression data which further demonstrate the value of our approach.

Minimum Distance Estimation for Robust High-Dimensional Regression

We propose a minimum distance estimation method for robust regression in sparse high-dimensional settings. The traditional likelihood-based estimators lack resilience against outliers, a critical issue when dealing with high-dimensional noisy data. Our method, Minimum Distance Lasso (MD-Lasso), combines minimum distance functionals, customarily used in nonparametric estimation for their robustness, with l1-regularization for high-dimensional regression. The geometry of MD-Lasso is key to its consistency and robustness. The estimator is governed by a scaling parameter that caps the influence of outliers: the loss per observation is locally convex and close to quadratic for small squared residuals, and flattens for squared residuals larger than the scaling parameter. As the parameter approaches infinity, the estimator becomes equivalent to least-squares Lasso. MD-Lasso enjoys fast convergence rates under mild conditions on the model error distribution, which hold for any of the solutions in a convexity region around the true parameter and in certain cases for every solution. Remarkably, a first-order optimization method is able to produce iterates very close to the consistent solutions, with geometric convergence and regardless of the initialization. A connection is established with re-weighted least-squares that intuitively explains MD-Lasso robustness. The merits of our method are demonstrated through simulation and eQTL data analysis.