Learning task structure via sparsity grouped multitask learning
Paper and Code
Sep 15, 2017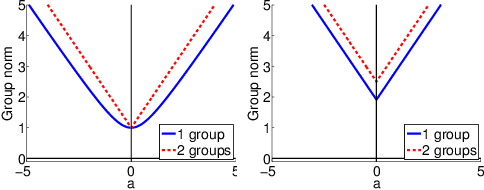

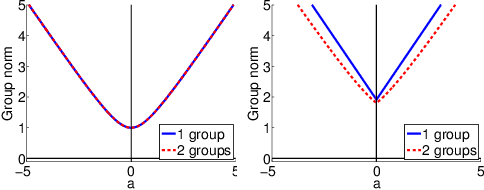
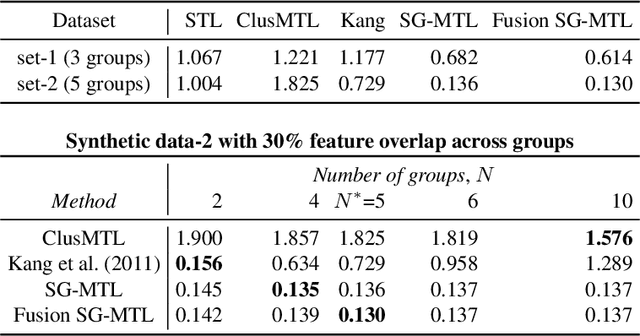
Sparse mapping has been a key methodology in many high-dimensional scientific problems. When multiple tasks share the set of relevant features, learning them jointly in a group drastically improves the quality of relevant feature selection. However, in practice this technique is used limitedly since such grouping information is usually hidden. In this paper, our goal is to recover the group structure on the sparsity patterns and leverage that information in the sparse learning. Toward this, we formulate a joint optimization problem in the task parameter and the group membership, by constructing an appropriate regularizer to encourage sparse learning as well as correct recovery of task groups. We further demonstrate that our proposed method recovers groups and the sparsity patterns in the task parameters accurately by extensive experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge