Invariant-Stratified Propagation for Expressive Graph Neural Networks

Graph Neural Networks (GNNs) face fundamental limitations in expressivity and capturing structural heterogeneity. Standard message-passing architectures are constrained by the 1-dimensional Weisfeiler-Leman (1-WL) test, unable to distinguish graphs beyond degree sequences, and aggregate information uniformly from neighbors, failing to capture how nodes occupy different structural positions within higher-order patterns. While methods exist to achieve higher expressivity, they incur prohibitive computational costs and lack unified frameworks for flexibly encoding diverse structural properties. To address these limitations, we introduce Invariant-Stratified Propagation (ISP), a framework comprising both a novel WL variant (ISP-WL) and its efficient neural network implementation (ISPGNN). ISP stratifies nodes according to graph invariants, processing them in hierarchical strata that reveal structural distinctions invisible to 1-WL. Through hierarchical structural heterogeneity encoding, ISP quantifies differences in nodes' structural positions within higher-order patterns, distinguishing interactions where participants occupy different roles from those with uniform participation. We provide formal theoretical analysis establishing enhanced expressivity beyond 1-WL, convergence guarantees, and inherent resistance to oversmoothing. Extensive experiments across graph classification, node classification, and influence estimation demonstrate consistent improvements over standard architectures and state-of-the-art expressive baselines.

Flowette: Flow Matching with Graphette Priors for Graph Generation

We study generative modeling of graphs with recurring subgraph motifs. We propose Flowette, a continuous flow matching framework, that employs a graph neural network based transformer to learn a velocity field defined over graph representations with node and edge attributes. Our model preserves topology through optimal transport based coupling, and long-range structural dependencies through regularisation. To incorporate domain driven structural priors, we introduce graphettes, a new probabilistic family of graph structure models that generalize graphons via controlled structural edits for motifs like rings, stars and trees. We theoretically analyze the coupling, invariance, and structural properties of the proposed framework, and empirically evaluate it on synthetic and small-molecule graph generation tasks. Flowette demonstrates consistent improvements, highlighting the effectiveness of combining structural priors with flow-based training for modeling complex graph distributions.

Beyond Fixed Depth: Adaptive Graph Neural Networks for Node Classification Under Varying Homophily

Graph Neural Networks (GNNs) have achieved significant success in addressing node classification tasks. However, the effectiveness of traditional GNNs degrades on heterophilic graphs, where connected nodes often belong to different labels or properties. While recent work has introduced mechanisms to improve GNN performance under heterophily, certain key limitations still exist. Most existing models apply a fixed aggregation depth across all nodes, overlooking the fact that nodes may require different propagation depths based on their local homophily levels and neighborhood structures. Moreover, many methods are tailored to either homophilic or heterophilic settings, lacking the flexibility to generalize across both regimes. To address these challenges, we develop a theoretical framework that links local structural and label characteristics to information propagation dynamics at the node level. Our analysis shows that optimal aggregation depth varies across nodes and is critical for preserving class-discriminative information. Guided by this insight, we propose a novel adaptive-depth GNN architecture that dynamically selects node-specific aggregation depths using theoretically grounded metrics. Our method seamlessly adapts to both homophilic and heterophilic patterns within a unified model. Extensive experiments demonstrate that our approach consistently enhances the performance of standard GNN backbones across diverse benchmarks.

Graph Self-Supervised Learning with Learnable Structural and Positional Encodings

Traditional Graph Self-Supervised Learning (GSSL) struggles to capture complex structural properties well. This limitation stems from two main factors: (1) the inadequacy of conventional Graph Neural Networks (GNNs) in representing sophisticated topological features, and (2) the focus of self-supervised learning solely on final graph representations. To address these issues, we introduce \emph{GenHopNet}, a GNN framework that integrates a $k$-hop message-passing scheme, enhancing its ability to capture local structural information without explicit substructure extraction. We theoretically demonstrate that \emph{GenHopNet} surpasses the expressiveness of the classical Weisfeiler-Lehman (WL) test for graph isomorphism. Furthermore, we propose a structural- and positional-aware GSSL framework that incorporates topological information throughout the learning process. This approach enables the learning of representations that are both sensitive to graph topology and invariant to specific structural and feature augmentations. Comprehensive experiments on graph classification datasets, including those designed to test structural sensitivity, show that our method consistently outperforms the existing approaches and maintains computational efficiency. Our work significantly advances GSSL's capability in distinguishing graphs with similar local structures but different global topologies.

A Regularized Wasserstein Framework for Graph Kernels

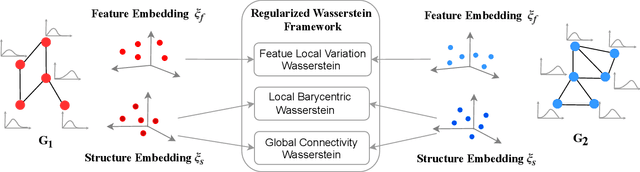
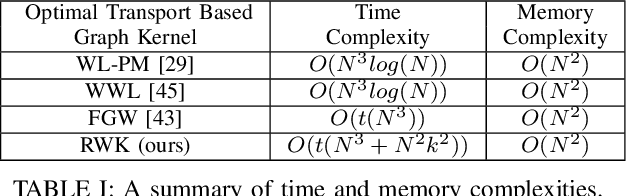
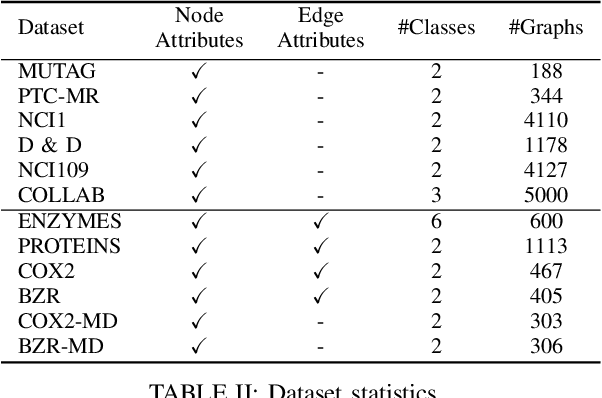
We propose a learning framework for graph kernels, which is theoretically grounded on regularizing optimal transport. This framework provides a novel optimal transport distance metric, namely Regularized Wasserstein (RW) discrepancy, which can preserve both features and structure of graphs via Wasserstein distances on features and their local variations, local barycenters and global connectivity. Two strongly convex regularization terms are introduced to improve the learning ability. One is to relax an optimal alignment between graphs to be a cluster-to-cluster mapping between their locally connected vertices, thereby preserving the local clustering structure of graphs. The other is to take into account node degree distributions in order to better preserve the global structure of graphs. We also design an efficient algorithm to enable a fast approximation for solving the optimization problem. Theoretically, our framework is robust and can guarantee the convergence and numerical stability in optimization. We have empirically validated our method using 12 datasets against 16 state-of-the-art baselines. The experimental results show that our method consistently outperforms all state-of-the-art methods on all benchmark databases for both graphs with discrete attributes and graphs with continuous attributes.

ErGAN: Generative Adversarial Networks for Entity Resolution

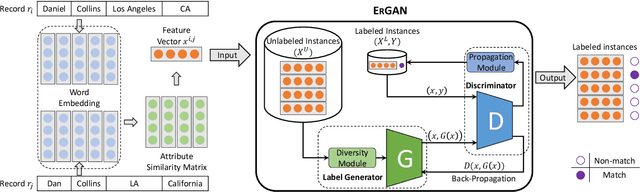
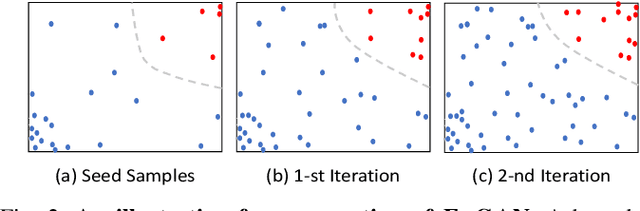
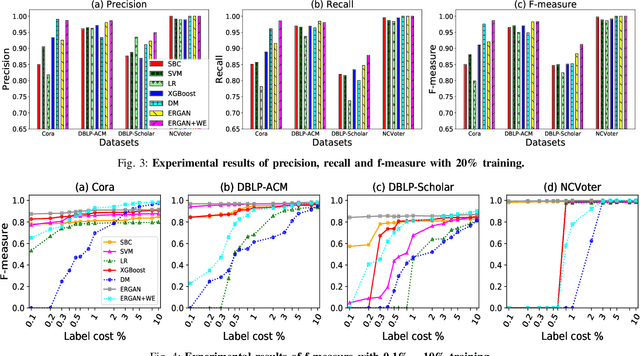
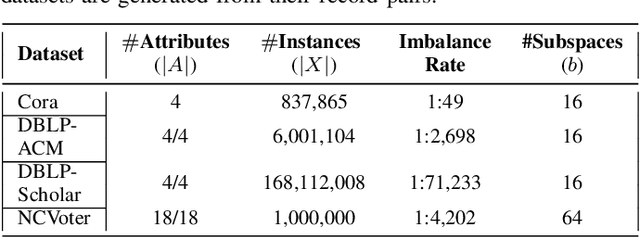
Entity resolution targets at identifying records that represent the same real-world entity from one or more datasets. A major challenge in learning-based entity resolution is how to reduce the label cost for training. Due to the quadratic nature of record pair comparison, labeling is a costly task that often requires a significant effort from human experts. Inspired by recent advances of generative adversarial network (GAN), we propose a novel deep learning method, called ErGAN, to address the challenge. ErGAN consists of two key components: a label generator and a discriminator which are optimized alternatively through adversarial learning. To alleviate the issues of overfitting and highly imbalanced distribution, we design two novel modules for diversity and propagation, which can greatly improve the model generalization power. We have conducted extensive experiments to empirically verify the labeling and learning efficiency of ErGAN. The experimental results show that ErGAN beats the state-of-the-art baselines, including unsupervised, semi-supervised, and unsupervised learning methods.

DFNets: Spectral CNNs for Graphs with Feedback-Looped Filters

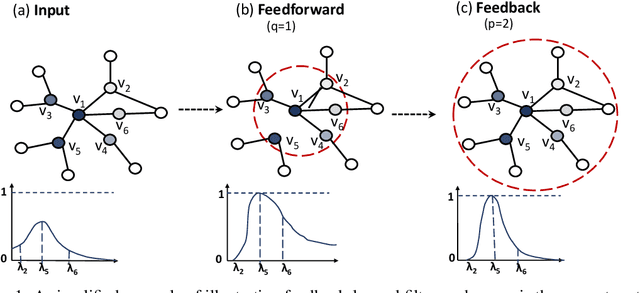
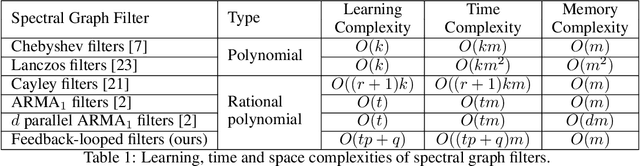
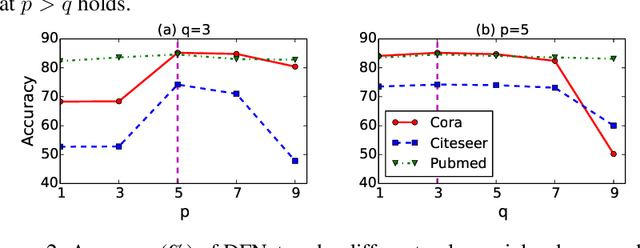
We propose a novel spectral convolutional neural network (CNN) model on graph structured data, namely Distributed Feedback-Looped Networks (DFNets). This model is incorporated with a robust class of spectral graph filters, called feedback-looped filters, to provide better localization on vertices, while still attaining fast convergence and linear memory requirements. Theoretically, feedback-looped filters can guarantee convergence w.r.t. a specified error bound, and be applied universally to any graph without knowing its structure. Furthermore, the propagation rule of this model can diversify features from the preceding layers to produce strong gradient flows. We have evaluated our model using two benchmark tasks: semi-supervised document classification on citation networks and semi-supervised entity classification on a knowledge graph. The experimental results show that our model considerably outperforms the state-of-the-art methods in both benchmark tasks over all datasets.