A Regularized Wasserstein Framework for Graph Kernels
Paper and Code
Oct 08, 2021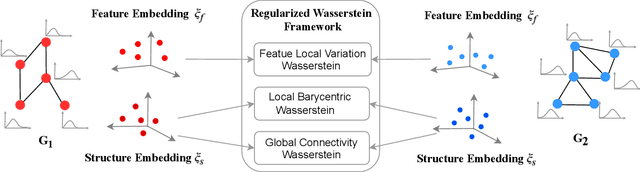

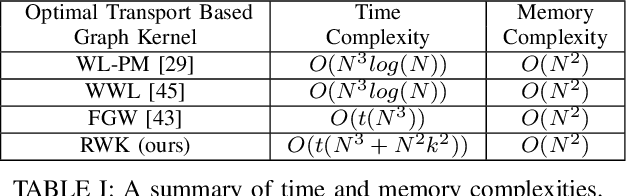
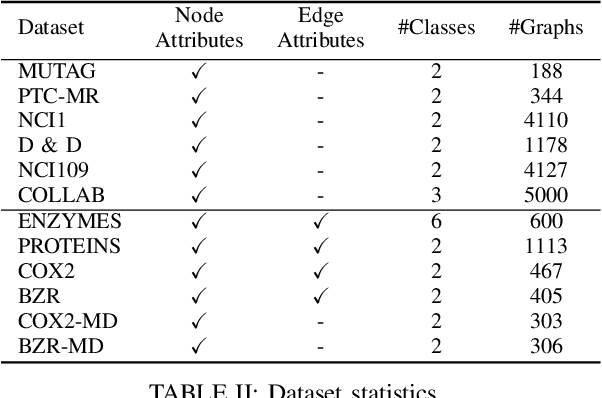
We propose a learning framework for graph kernels, which is theoretically grounded on regularizing optimal transport. This framework provides a novel optimal transport distance metric, namely Regularized Wasserstein (RW) discrepancy, which can preserve both features and structure of graphs via Wasserstein distances on features and their local variations, local barycenters and global connectivity. Two strongly convex regularization terms are introduced to improve the learning ability. One is to relax an optimal alignment between graphs to be a cluster-to-cluster mapping between their locally connected vertices, thereby preserving the local clustering structure of graphs. The other is to take into account node degree distributions in order to better preserve the global structure of graphs. We also design an efficient algorithm to enable a fast approximation for solving the optimization problem. Theoretically, our framework is robust and can guarantee the convergence and numerical stability in optimization. We have empirically validated our method using 12 datasets against 16 state-of-the-art baselines. The experimental results show that our method consistently outperforms all state-of-the-art methods on all benchmark databases for both graphs with discrete attributes and graphs with continuous attributes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge