Ashley Lyons
Spatial images from temporal data
Dec 02, 2019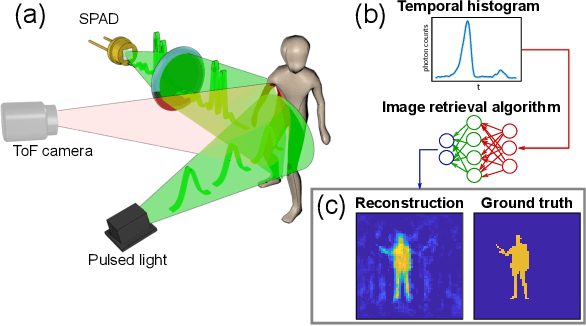
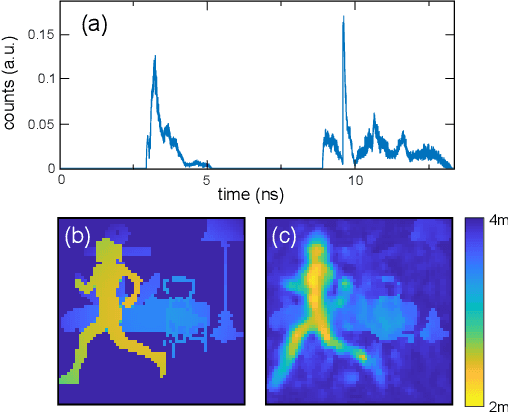
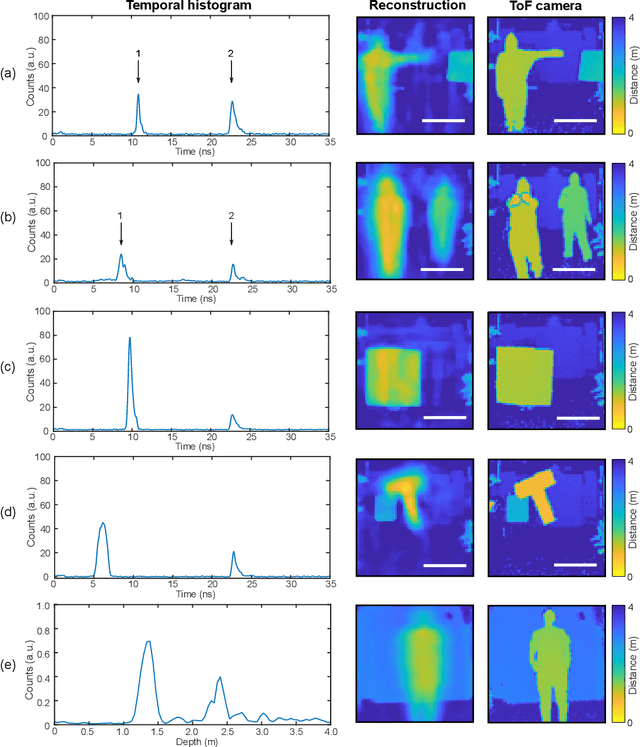
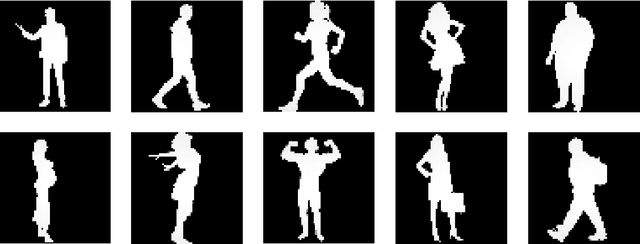
Abstract:Traditional paradigms for imaging rely on the use of spatial structure either in the detector (pixels arrays) or in the illumination (patterned light). Removal of spatial structure in the detector or illumination, i.e. imaging with just a single-point sensor, would require solving a very strongly ill-posed inverse retrieval problem that to date has not been solved. Here we demonstrate a data-driven approach in which full 3D information is obtained with just a single-point, single-photon avalanche diode that records the arrival time of photons reflected from a scene that is illuminated with short pulses of light. Imaging with single-point time-of-flight (temporal) data opens new routes in terms of speed, size, and functionality. As an example, we show how the training based on an optical time-of-flight camera enables a compact radio-frequency impulse RADAR transceiver to provide 3D images.
Variational Inference for Computational Imaging Inverse Problems
Apr 12, 2019



Abstract:We introduce a method to infer a variational approximation to the posterior distribution of solutions in computational imaging inverse problems. Machine learning methods applied to computational imaging have proven very successful, but have so far largely focused on retrieving a single optimal solution for a given task. Such retrieval is arguably an incomplete description of the solution space, as in ill-posed inverse problems there may be many similarly likely reconstructions. We minimise an upper bound on the divergence between our approximate distribution and the true intractable posterior, thereby obtaining a probabilistic description of the solution space in imaging inverse problems with empirical prior. We demonstrate the advantage of our technique in quantitative simulations with the CelebA dataset and common image reconstruction tasks. We then apply our method to two of the currently most challenging problems in experimental optics: imaging through highly scattering media and imaging through multi-modal optical fibres. In both settings we report state of the art reconstructions, while providing new capabilities, such as estimation of error-bars and visualisation of multiple likely reconstructions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge