Hidden Traveling Waves bind Working Memory Variables in Recurrent Neural Networks

Traveling waves are a fundamental phenomenon in the brain, playing a crucial role in short-term information storage. In this study, we leverage the concept of traveling wave dynamics within a neural lattice to formulate a theoretical model of neural working memory, study its properties, and its real world implications in AI. The proposed model diverges from traditional approaches, which assume information storage in static, register-like locations updated by interference. Instead, the model stores data as waves that is updated by the wave's boundary conditions. We rigorously examine the model's capabilities in representing and learning state histories, which are vital for learning history-dependent dynamical systems. The findings reveal that the model reliably stores external information and enhances the learning process by addressing the diminishing gradient problem. To understand the model's real-world applicability, we explore two cases: linear boundary condition and non-linear, self-attention-driven boundary condition. The experiments reveal that the linear scenario is effectively learned by Recurrent Neural Networks (RNNs) through backpropagation when modeling history-dependent dynamical systems. Conversely, the non-linear scenario parallels the autoregressive loop of an attention-only transformer. Collectively, our findings suggest the broader relevance of traveling waves in AI and its potential in advancing neural network architectures.

Model Complexity of Program Phases

In resource limited computing systems, sequence prediction models must operate under tight constraints. Various models are available that cater to prediction under these conditions that in some way focus on reducing the cost of implementation. These resource constrained sequence prediction models, in practice, exhibit a fundamental tradeoff between the cost of implementation and the quality of its predictions. This fundamental tradeoff seems to be largely unexplored for models for different tasks. Here we formulate the necessary theory and an associated empirical procedure to explore this tradeoff space for a particular family of machine learning models such as deep neural networks. We anticipate that the knowledge of the behavior of this tradeoff may be beneficial in understanding the theoretical and practical limits of creation and deployment of models for resource constrained tasks.

Episodic Memory Theory for the Mechanistic Interpretation of Recurrent Neural Networks

Understanding the intricate operations of Recurrent Neural Networks (RNNs) mechanistically is pivotal for advancing their capabilities and applications. In this pursuit, we propose the Episodic Memory Theory (EMT), illustrating that RNNs can be conceptualized as discrete-time analogs of the recently proposed General Sequential Episodic Memory Model. To substantiate EMT, we introduce a novel set of algorithmic tasks tailored to probe the variable binding behavior in RNNs. Utilizing the EMT, we formulate a mathematically rigorous circuit that facilitates variable binding in these tasks. Our empirical investigations reveal that trained RNNs consistently converge to the variable binding circuit, thus indicating universality in the dynamics of RNNs. Building on these findings, we devise an algorithm to define a privileged basis, which reveals hidden neurons instrumental in the temporal storage and composition of variables, a mechanism vital for the successful generalization in these tasks. We show that the privileged basis enhances the interpretability of the learned parameters and hidden states of RNNs. Our work represents a step toward demystifying the internal mechanisms of RNNs and, for computational neuroscience, serves to bridge the gap between artificial neural networks and neural memory models.

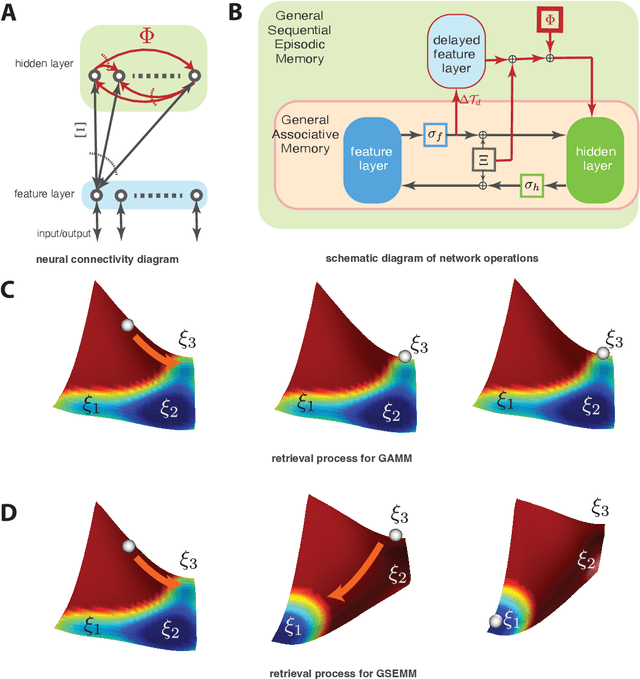
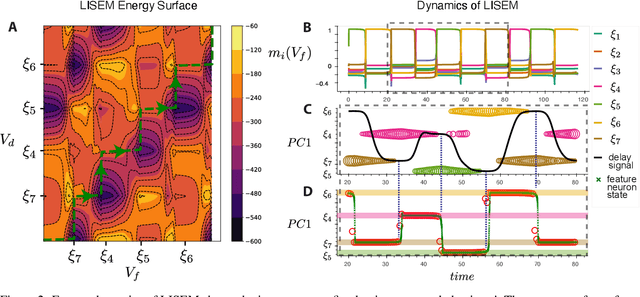
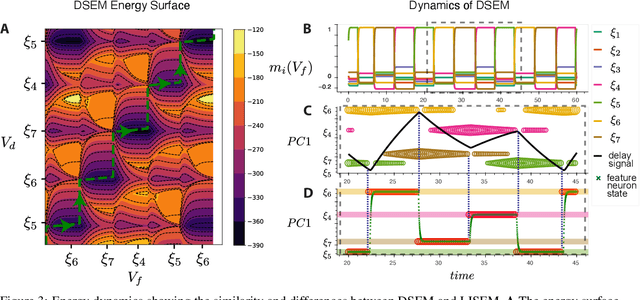
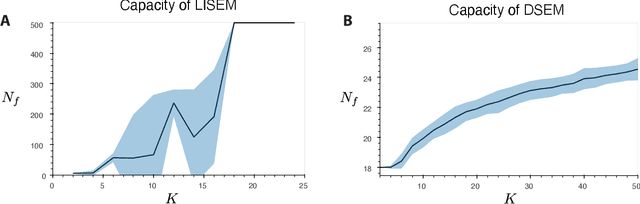
Energy-based General Sequential Episodic Memory Networks at the Adiabatic Limit

The General Associative Memory Model (GAMM) has a constant state-dependant energy surface that leads the output dynamics to fixed points, retrieving single memories from a collection of memories that can be asynchronously preloaded. We introduce a new class of General Sequential Episodic Memory Models (GSEMM) that, in the adiabatic limit, exhibit temporally changing energy surface, leading to a series of meta-stable states that are sequential episodic memories. The dynamic energy surface is enabled by newly introduced asymmetric synapses with signal propagation delays in the network's hidden layer. We study the theoretical and empirical properties of two memory models from the GSEMM class, differing in their activation functions. LISEM has non-linearities in the feature layer, whereas DSEM has non-linearity in the hidden layer. In principle, DSEM has a storage capacity that grows exponentially with the number of neurons in the network. We introduce a learning rule for the synapses based on the energy minimization principle and show it can learn single memories and their sequential relationships online. This rule is similar to the Hebbian learning algorithm and Spike-Timing Dependent Plasticity (STDP), which describe conditions under which synapses between neurons change strength. Thus, GSEMM combines the static and dynamic properties of episodic memory under a single theoretical framework and bridges neuroscience, machine learning, and artificial intelligence.

A Study into the similarity in generator and discriminator in GAN architecture

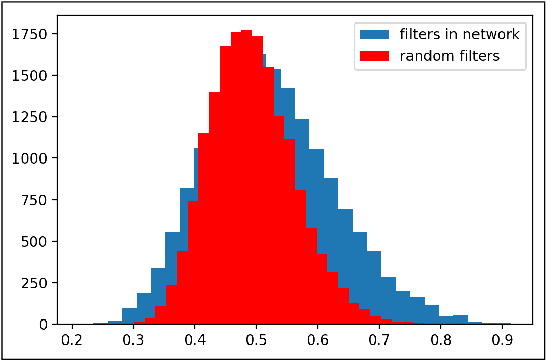
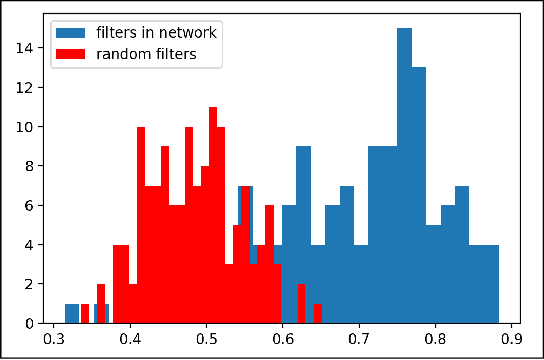
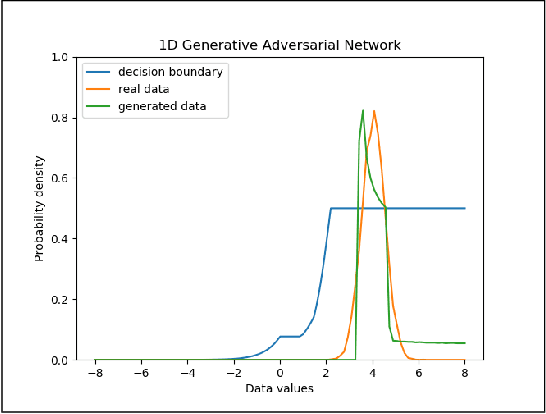
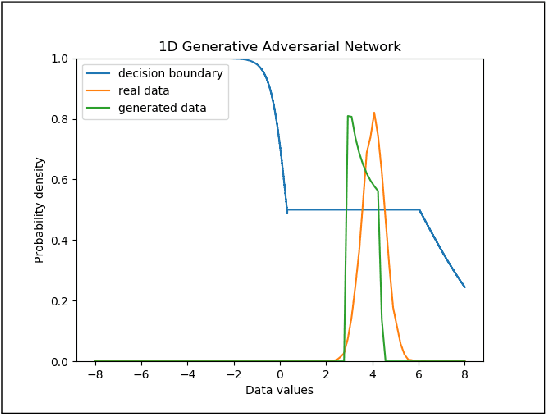
One popular generative model that has high-quality results is the Generative Adversarial Networks(GAN). This type of architecture consists of two separate networks that play against each other. The generator creates an output from the input noise that is given to it. The discriminator has the task of determining if the input to it is real or fake. This takes place constantly eventually leads to the generator modeling the target distribution. This paper includes a study into the actual weights learned by the network and a study into the similarity of the discriminator and generator networks. The paper also tries to leverage the similarity between these networks and shows that indeed both the networks may have a similar structure with experimental evidence with a novel shared architecture.