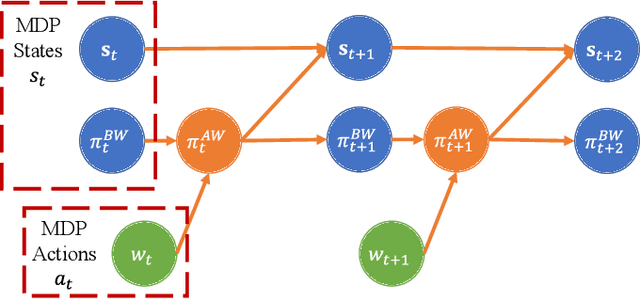
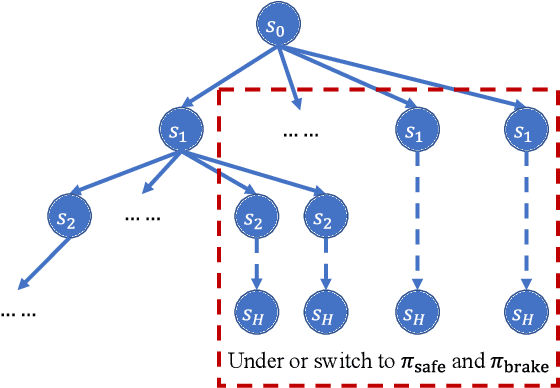
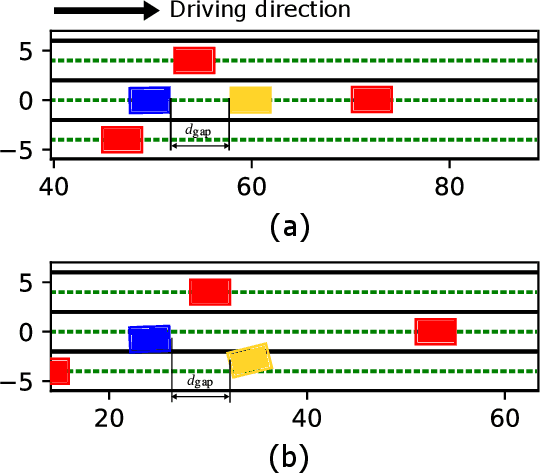
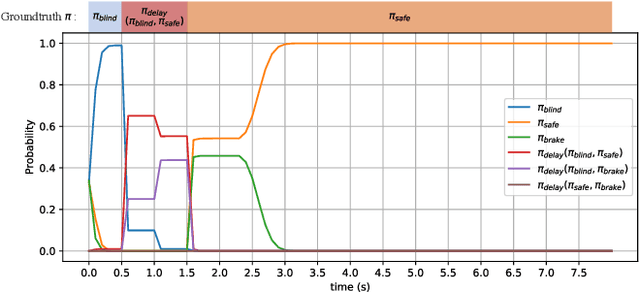
Optimal Driver Warning Generation in Dynamic Driving Environment

The driver warning system that alerts the human driver about potential risks during driving is a key feature of an advanced driver assistance system. Existing driver warning technologies, mainly the forward collision warning and unsafe lane change warning, can reduce the risk of collision caused by human errors. However, the current design methods have several major limitations. Firstly, the warnings are mainly generated in a one-shot manner without modeling the ego driver's reactions and surrounding objects, which reduces the flexibility and generality of the system over different scenarios. Additionally, the triggering conditions of warning are mostly rule-based threshold-checking given the current state, which lacks the prediction of the potential risk in a sufficiently long future horizon. In this work, we study the problem of optimally generating driver warnings by considering the interactions among the generated warning, the driver behavior, and the states of ego and surrounding vehicles on a long horizon. The warning generation problem is formulated as a partially observed Markov decision process (POMDP). An optimal warning generation framework is proposed as a solution to the proposed POMDP. The simulation experiments demonstrate the superiority of the proposed solution to the existing warning generation methods.

Bayesian Learning for Dynamic Inference

The traditional statistical inference is static, in the sense that the estimate of the quantity of interest does not affect the future evolution of the quantity. In some sequential estimation problems however, the future values of the quantity to be estimated depend on the estimate of its current value. This type of estimation problems has been formulated as the dynamic inference problem. In this work, we formulate the Bayesian learning problem for dynamic inference, where the unknown quantity-generation model is assumed to be randomly drawn according to a random model parameter. We derive the optimal Bayesian learning rules, both offline and online, to minimize the inference loss. Moreover, learning for dynamic inference can serve as a meta problem, such that all familiar machine learning problems, including supervised learning, imitation learning and reinforcement learning, can be cast as its special cases or variants. Gaining a good understanding of this unifying meta problem thus sheds light on a broad spectrum of machine learning problems as well.

Dynamic Inference

Traditional statistical estimation, or statistical inference in general, is static, in the sense that the estimate of the quantity of interest does not change the future evolution of the quantity. In some sequential estimation problems however, we encounter the situation where the future values of the quantity to be estimated depend on the estimate of its current value. Examples include stock price prediction by big investors, interactive product recommendation, and behavior prediction in multi-agent systems. We may call such problems as dynamic inference. In this work, a formulation of this problem under a Bayesian probabilistic framework is given, and the optimal estimation strategy is derived as the solution to minimize the overall inference loss. How the optimal estimation strategy works is illustrated through two examples, stock trend prediction and vehicle behavior prediction. When the underlying models for dynamic inference are unknown, we can consider the problem of learning for dynamic inference. This learning problem can potentially unify several familiar machine learning problems, including supervised learning, imitation learning, and reinforcement learning.

Continuity of Generalized Entropy and Statistical Learning

We study the continuity property of the generalized entropy as a functional of the underlying probability distribution, defined with an action space and a loss function, and use this property to answer the basic questions in statistical learning theory, the excess risk analyses for various learning methods. We first derive upper and lower bounds for the entropy difference of two distributions in terms of several commonly used $f$-divergences, the Wasserstein distance, and a distance that depends on the action space and the loss function. Examples are given along with the discussion of each general result, comparisons are made with the existing entropy difference bounds, and new mutual information upper bounds are derived based on the new results. We then apply the entropy difference bounds to the theory of statistical learning. It is shown that the excess risks in the two popular learning paradigms, the frequentist learning and the Bayesian learning, both can be studied with the continuity property of different forms of the generalized entropy. The analysis is then extended to the continuity of generalized conditional entropy. The extension provides performance bounds for Bayes decision making with mismatched distributions. It also leads to excess risk bounds for a third paradigm of learning, where the decision rule is optimally designed under the projection of the empirical distribution to a predefined family of distributions. We thus establish a unified method of excess risk analysis for the three major paradigms of statistical learning, through the continuity of generalized entropy.

Minimum Excess Risk in Bayesian Learning

We analyze the best achievable performance of Bayesian learning under generative models by defining and upper-bounding the minimum excess risk (MER): the gap between the minimum expected loss attainable by learning from data and the minimum expected loss that could be achieved if the model realization were known. The definition of MER provides a principled way to define different notions of uncertainties in Bayesian learning, including the aleatoric uncertainty and the minimum epistemic uncertainty. Two methods for deriving upper bounds for the MER are presented. The first method, generally suitable for Bayesian learning with a parametric generative model, upper-bounds the MER by the conditional mutual information between the model parameters and the quantity being predicted given the observed data. It allows us to quantify the rate at which the MER decays to zero as more data becomes available. The second method, particularly suitable for Bayesian learning with a parametric predictive model, relates the MER to the deviation of the posterior predictive distribution from the true predictive model, and further to the minimum estimation error of the model parameters from data. It explicitly shows how the uncertainty in model parameter estimation translates to the MER and to the final prediction uncertainty. We also extend the definition and analysis of MER to the setting with multiple parametric model families and the setting with nonparametric models. Along the discussions we draw some comparisons between the MER in Bayesian learning and the excess risk in frequentist learning.

Information-theoretic analysis of generalization capability of learning algorithms

We derive upper bounds on the generalization error of a learning algorithm in terms of the mutual information between its input and output. The bounds provide an information-theoretic understanding of generalization in learning problems, and give theoretical guidelines for striking the right balance between data fit and generalization by controlling the input-output mutual information. We propose a number of methods for this purpose, among which are algorithms that regularize the ERM algorithm with relative entropy or with random noise. Our work extends and leads to nontrivial improvements on the recent results of Russo and Zou.