Dynamic Inference
Paper and Code
Nov 30, 2021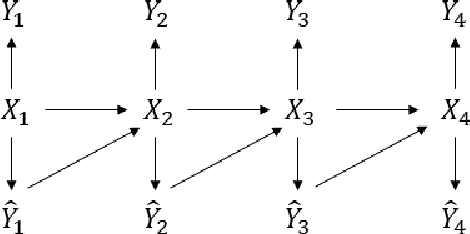
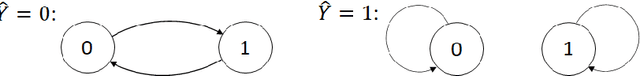
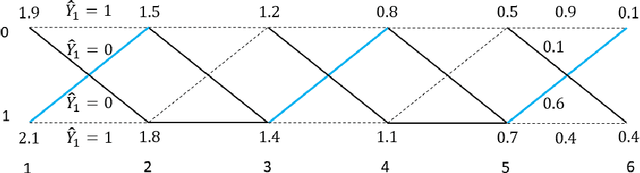
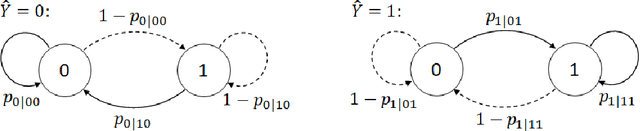
Traditional statistical estimation, or statistical inference in general, is static, in the sense that the estimate of the quantity of interest does not change the future evolution of the quantity. In some sequential estimation problems however, we encounter the situation where the future values of the quantity to be estimated depend on the estimate of its current value. Examples include stock price prediction by big investors, interactive product recommendation, and behavior prediction in multi-agent systems. We may call such problems as dynamic inference. In this work, a formulation of this problem under a Bayesian probabilistic framework is given, and the optimal estimation strategy is derived as the solution to minimize the overall inference loss. How the optimal estimation strategy works is illustrated through two examples, stock trend prediction and vehicle behavior prediction. When the underlying models for dynamic inference are unknown, we can consider the problem of learning for dynamic inference. This learning problem can potentially unify several familiar machine learning problems, including supervised learning, imitation learning, and reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge