MMSE Channel Estimation in Large-Scale MIMO: Improved Robustness with Reduced Complexity

Large-scale MIMO systems with a massive number N of individually controlled antennas pose significant challenges for minimum mean square error (MMSE) channel estimation, based on uplink pilots. The major ones arise from the computational complexity, which scales with $N^3$, and from the need for accurate knowledge of the channel statistics. This paper aims to address both challenges by introducing reduced-complexity channel estimation methods that achieve the performance of MMSE in terms of estimation accuracy and uplink spectral efficiency while demonstrating improved robustness in practical scenarios where channel statistics must be estimated. This is achieved by exploiting the inherent structure of the spatial correlation matrix induced by the array geometry. Specifically, we use a Kronecker decomposition for uniform planar arrays and a well-suited circulant approximation for uniform linear arrays. By doing so, a significantly lower computational complexity is achieved, scaling as $N\sqrt{N}$ and $N\log N$ for squared planar arrays and linear arrays, respectively.

Holographic MIMO Communications: What is the benefit of closely spaced antennas?

Holographic MIMO refers to an array (possibly large) with a massive number of antennas that are individually controlled and densely deployed. The aim of this paper is to provide further insights into the advantages (if any) of having closely spaced antennas in the uplink and downlink of a multi-user Holographic MIMO system. To this end, we make use of the multiport communication theory, which ensures physically consistent uplink and downlink models. We first consider a simple uplink scenario with two side-by-side half-wavelength dipoles, two users and single path line-of-sight propagation, and show both analytically and numerically that the channel gain and average spectral efficiency depend strongly on the directions from which the signals are received and on the array matching network used. Numerical results are then used to extend the analysis to more practical scenarios with a larger number of dipoles and users. The case in which the antennas are densely packed in a space-constrained factor form is also considered. It turns out that the spectral efficiency increases as the antenna distance reduces thanks to the larger number of antennas that allow to collect more energy, not because of the mutual coupling.

DFT-Based Channel Estimation for Holographic MIMO

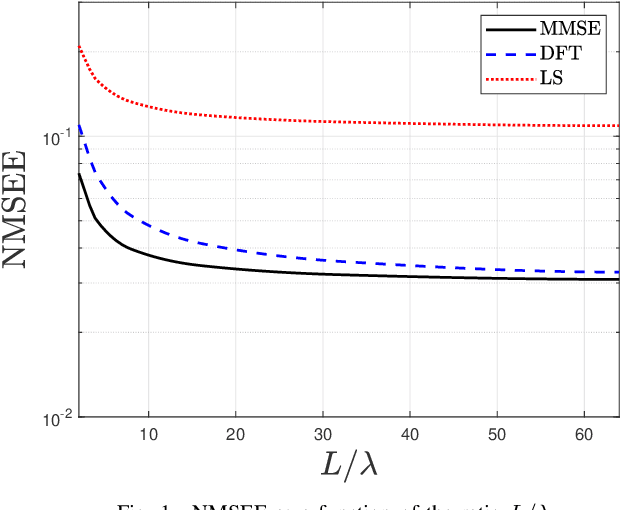
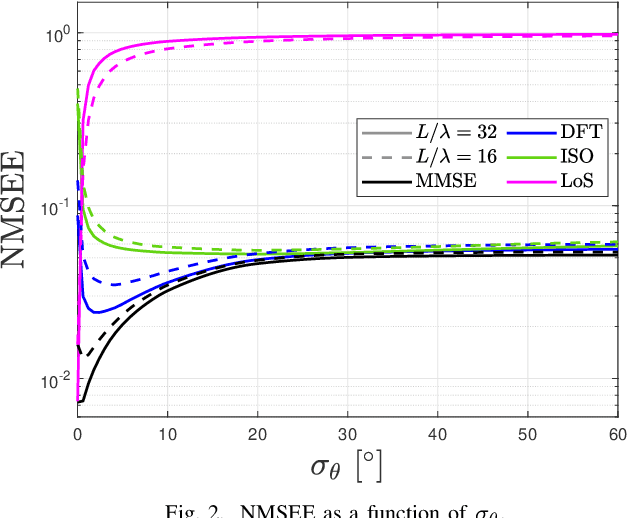
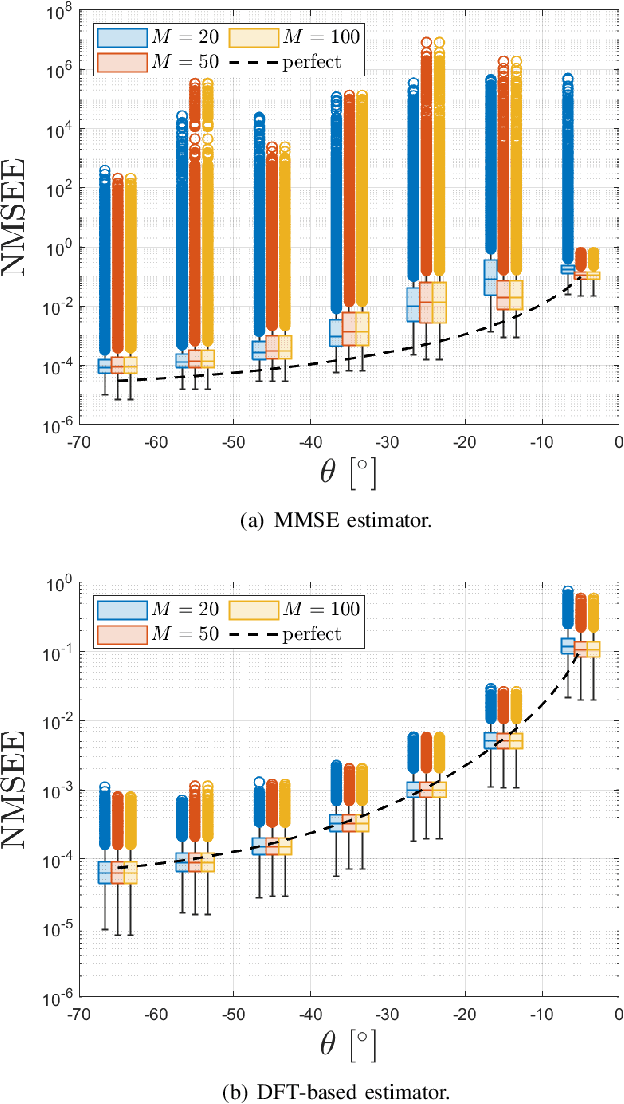
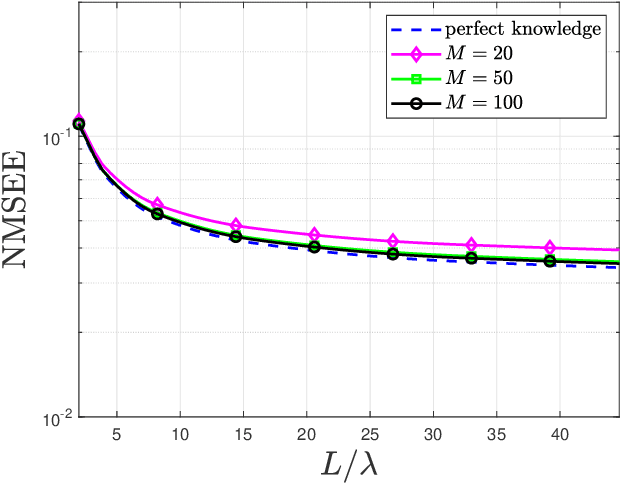
Holographic MIMO (hMIMO) systems with a massive number of individually controlled antennas N make minimum mean square error (MMSE) channel estimation particularly challenging, due to its computational complexity that scales as $N^3$ . This paper investigates uniform linear arrays and proposes a low-complexity method based on the discrete Fourier transform (DFT) approximation, which follows from replacing the covariance matrix by a suitable circulant matrix. Numerical results show that, already for arrays with moderate size (in the order of tens of wavelengths), it achieves the same performance of the optimal MMSE, but with a significant lower computational load that scales as $N \log N$. Interestingly, the proposed method provides also increased robustness in case of imperfect knowledge of the covariance matrix.

Performance analysis of WDM in LoS communications with arbitrary orientation and position

This letter focuses on the wavenumber-division-multiplexing (WDM) scheme that was recently proposed in [1] for line-of-sight communications between parallel spatially-continuous electromagnetic segments. Our aim is to analyze the performance of WDM, combined with different digital processing architectures, when the electromagnetic segments have an arbitrary orientation and position. To this end, we first show how the general electromagnetic MIMO (multiple-input multiple-output) model from [1] can be particularized to the case of interest and then use numerical results to evaluate the impact of system parameters (e.g., horizontal and vertical distances, azimuth and elevation orientations). It turns out that WDM performs satisfactorily also when the transmit and receive segments are not in boresight direction of each other.

Cramér-Rao Bounds for Near-Field Localization

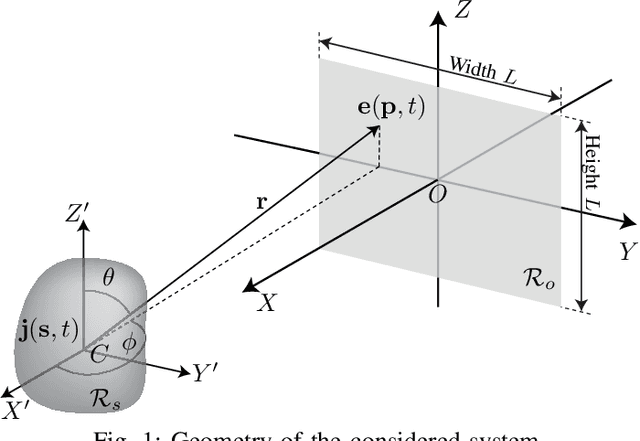
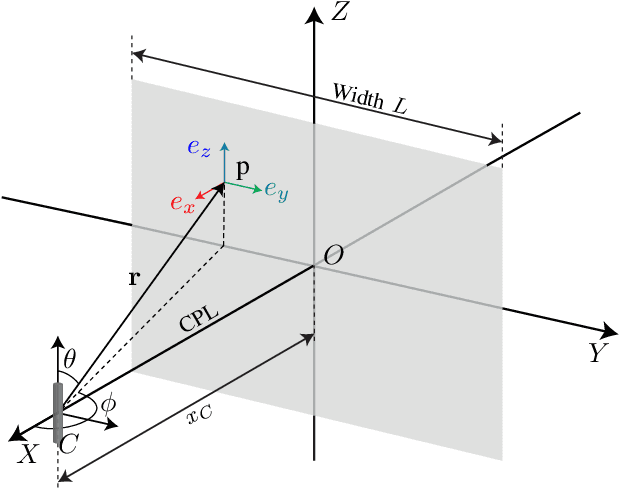
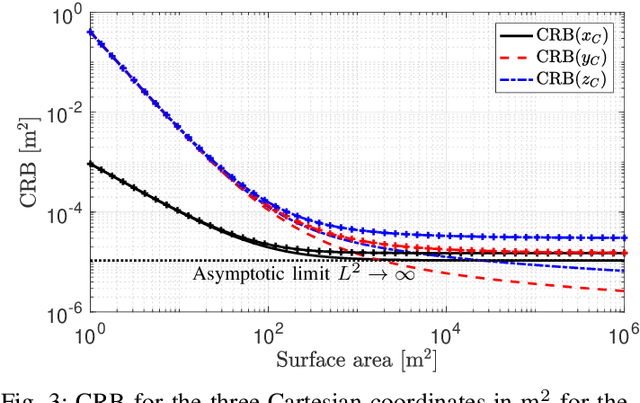
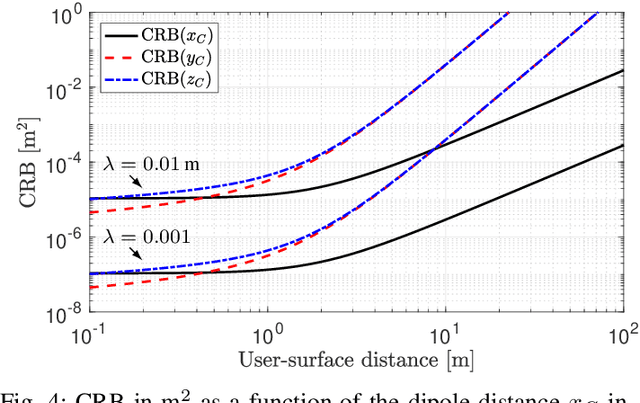
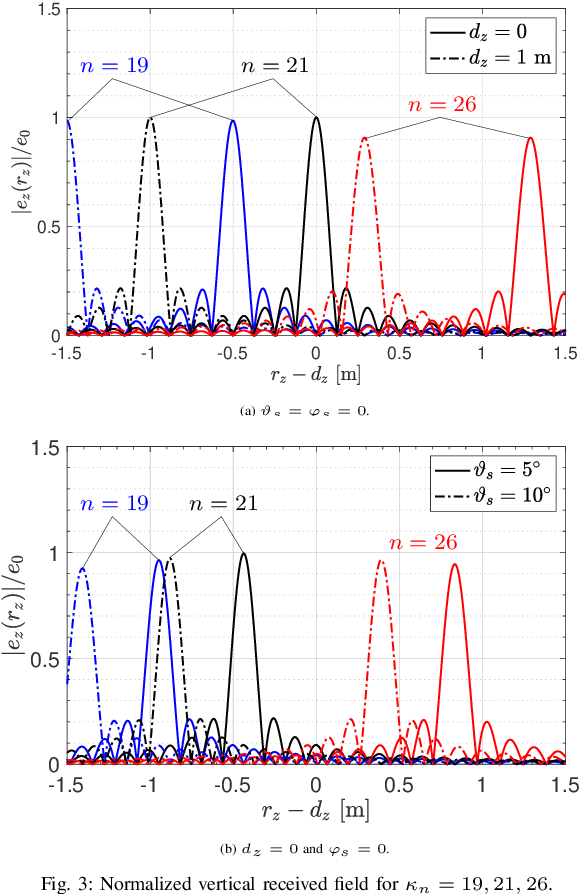
Multiple antenna arrays play a key role in wireless networks for communications but also localization and sensing. The use of large antenna arrays pushes towards the near-field propagation regime in which the wavefront is no longer plane but spherical. This allows to infer the position and orientation of an arbitrary source from the received signal without the need of using multiple anchor nodes. To understand the fundamental limits of large antenna arrays for localization, this paper fusions wave propagation theory with estimation theory, and computes the Cram\'er-Rao Bound (CRB) for the estimation of the three Cartesian coordinates of the source on the basis of the electromagnetic vector field, observed over a rectangular surface area. To simplify the analysis, we assume that the source is a dipole, whose center is located on the line perpendicular to the surface center, with an orientation a priori known. Numerical and asymptotic results are given to quantify the CRBs, and to gain insights into the effect of various system parameters on the ultimate estimation accuracy. It turns out that surfaces of practical size may guarantee a centimeter-level accuracy in the mmWave bands.