DFT-Based Channel Estimation for Holographic MIMO
Paper and Code
Jun 08, 2023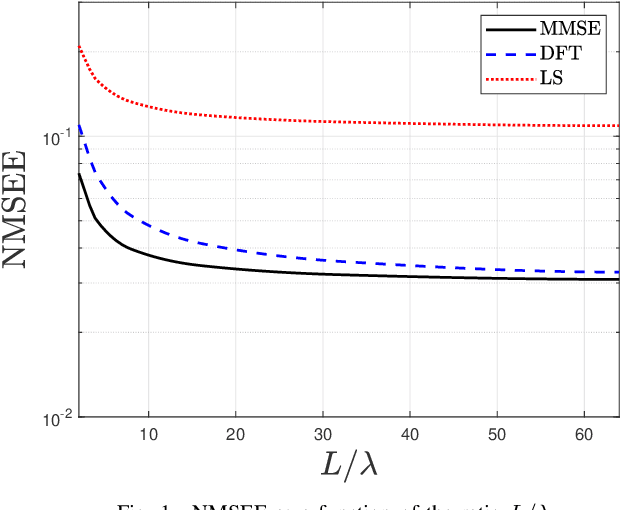
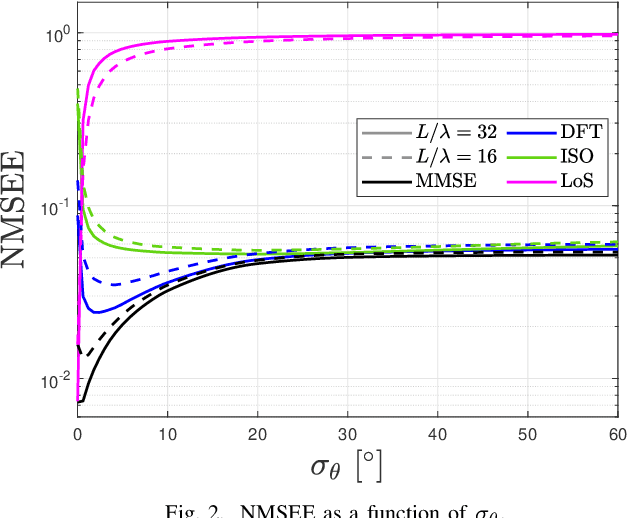
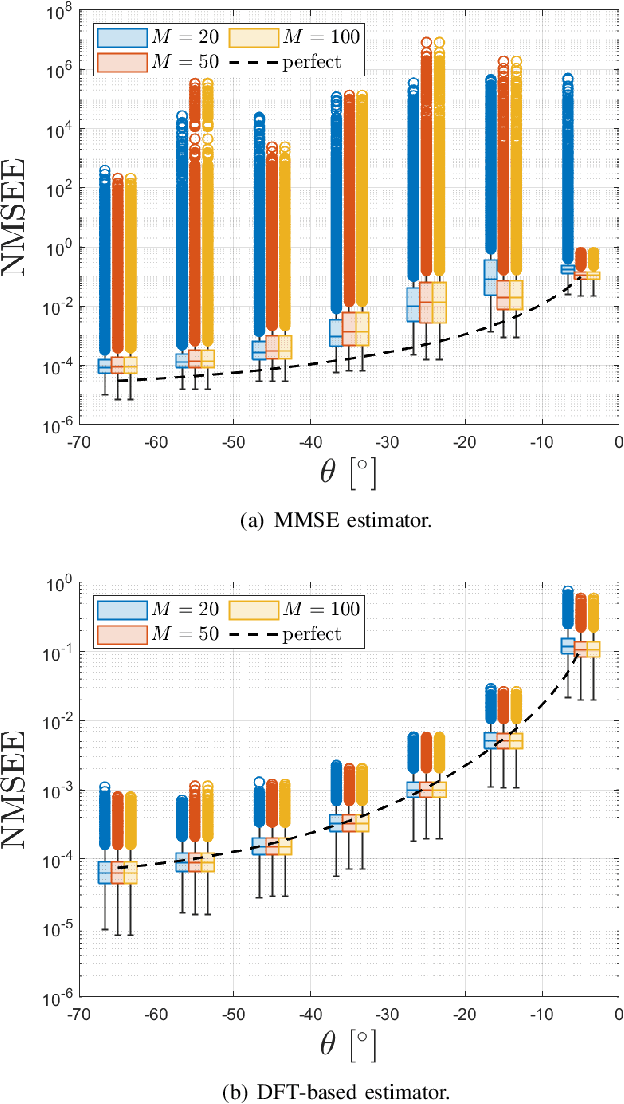
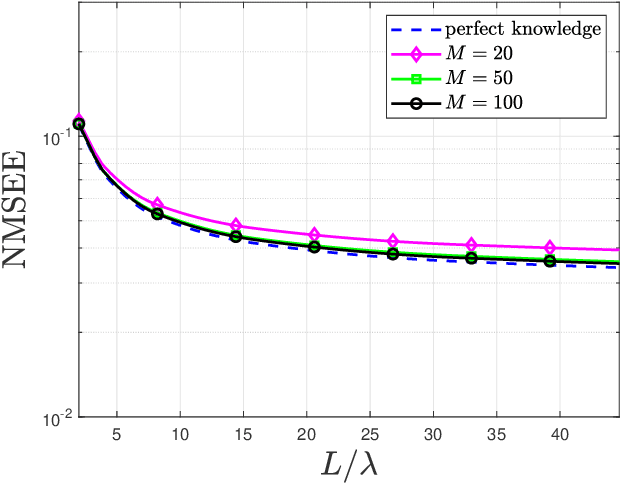
Holographic MIMO (hMIMO) systems with a massive number of individually controlled antennas N make minimum mean square error (MMSE) channel estimation particularly challenging, due to its computational complexity that scales as $N^3$ . This paper investigates uniform linear arrays and proposes a low-complexity method based on the discrete Fourier transform (DFT) approximation, which follows from replacing the covariance matrix by a suitable circulant matrix. Numerical results show that, already for arrays with moderate size (in the order of tens of wavelengths), it achieves the same performance of the optimal MMSE, but with a significant lower computational load that scales as $N \log N$. Interestingly, the proposed method provides also increased robustness in case of imperfect knowledge of the covariance matrix.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge