MMSE Channel Estimation in Large-Scale MIMO: Improved Robustness with Reduced Complexity
Paper and Code
Apr 04, 2024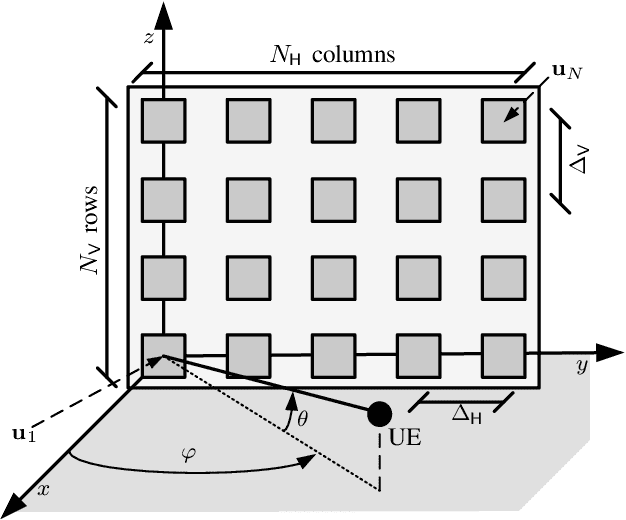
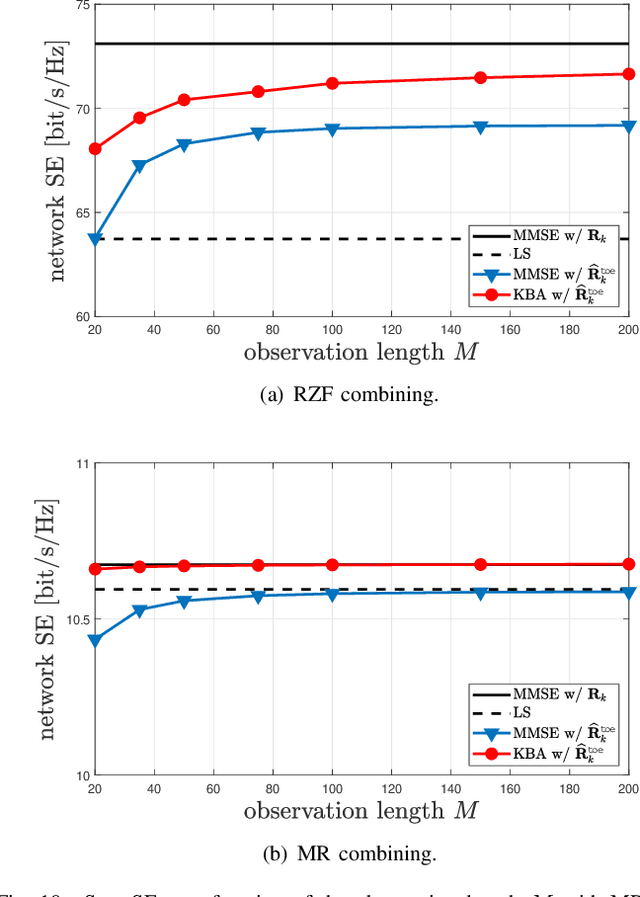
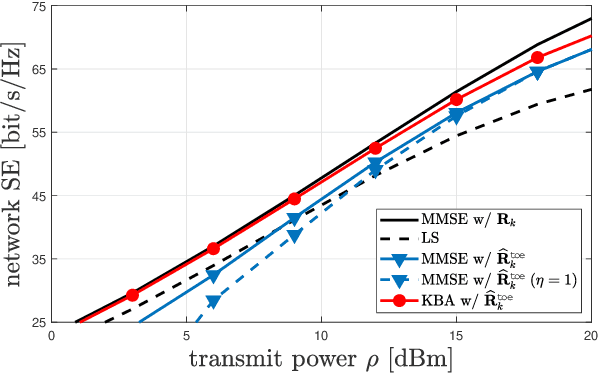
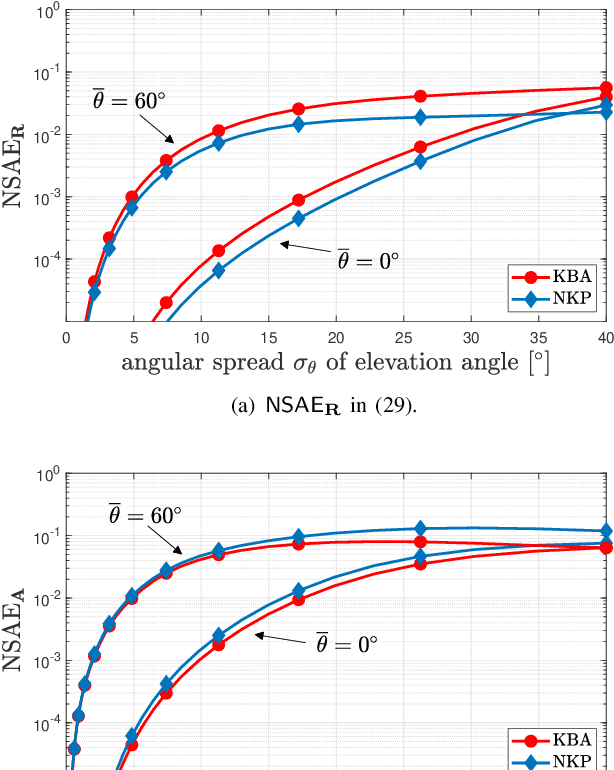
Large-scale MIMO systems with a massive number N of individually controlled antennas pose significant challenges for minimum mean square error (MMSE) channel estimation, based on uplink pilots. The major ones arise from the computational complexity, which scales with $N^3$, and from the need for accurate knowledge of the channel statistics. This paper aims to address both challenges by introducing reduced-complexity channel estimation methods that achieve the performance of MMSE in terms of estimation accuracy and uplink spectral efficiency while demonstrating improved robustness in practical scenarios where channel statistics must be estimated. This is achieved by exploiting the inherent structure of the spatial correlation matrix induced by the array geometry. Specifically, we use a Kronecker decomposition for uniform planar arrays and a well-suited circulant approximation for uniform linear arrays. By doing so, a significantly lower computational complexity is achieved, scaling as $N\sqrt{N}$ and $N\log N$ for squared planar arrays and linear arrays, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge