Anthony Degleris
Spatiotemporal Clustering with Neyman-Scott Processes via Connections to Bayesian Nonparametric Mixture Models
Jan 14, 2022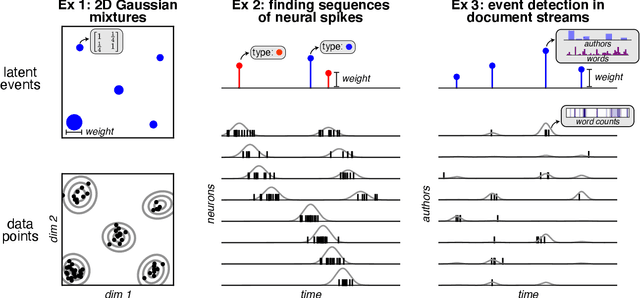

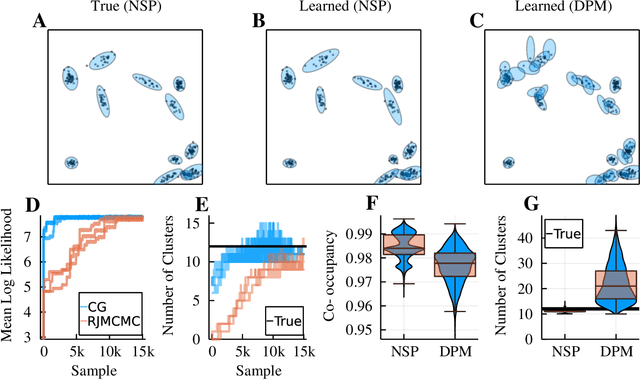
Abstract:Neyman-Scott processes (NSPs) are point process models that generate clusters of points in time or space. They are natural models for a wide range of phenomena, ranging from neural spike trains to document streams. The clustering property is achieved via a doubly stochastic formulation: first, a set of latent events is drawn from a Poisson process; then, each latent event generates a set of observed data points according to another Poisson process. This construction is similar to Bayesian nonparametric mixture models like the Dirichlet process mixture model (DPMM) in that the number of latent events (i.e. clusters) is a random variable, but the point process formulation makes the NSP especially well suited to modeling spatiotemporal data. While many specialized algorithms have been developed for DPMMs, comparatively fewer works have focused on inference in NSPs. Here, we present novel connections between NSPs and DPMMs, with the key link being a third class of Bayesian mixture models called mixture of finite mixture models (MFMMs). Leveraging this connection, we adapt the standard collapsed Gibbs sampling algorithm for DPMMs to enable scalable Bayesian inference on NSP models. We demonstrate the potential of Neyman-Scott processes on a variety of applications including sequence detection in neural spike trains and event detection in document streams.
Point process models for sequence detection in high-dimensional neural spike trains
Oct 10, 2020



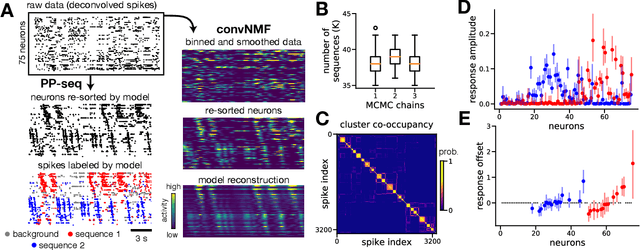
Abstract:Sparse sequences of neural spikes are posited to underlie aspects of working memory, motor production, and learning. Discovering these sequences in an unsupervised manner is a longstanding problem in statistical neuroscience. Promising recent work utilized a convolutive nonnegative matrix factorization model to tackle this challenge. However, this model requires spike times to be discretized, utilizes a sub-optimal least-squares criterion, and does not provide uncertainty estimates for model predictions or estimated parameters. We address each of these shortcomings by developing a point process model that characterizes fine-scale sequences at the level of individual spikes and represents sequence occurrences as a small number of marked events in continuous time. This ultra-sparse representation of sequence events opens new possibilities for spike train modeling. For example, we introduce learnable time warping parameters to model sequences of varying duration, which have been experimentally observed in neural circuits. We demonstrate these advantages on experimental recordings from songbird higher vocal center and rodent hippocampus.
Fast Convolutive Nonnegative Matrix Factorization Through Coordinate and Block Coordinate Updates
Jun 29, 2019


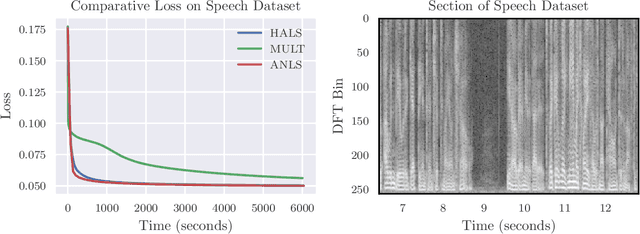
Abstract:Identifying recurring patterns in high-dimensional time series data is an important problem in many scientific domains. A popular model to achieve this is convolutive nonnegative matrix factorization (CNMF), which extends classic nonnegative matrix factorization (NMF) to extract short-lived temporal motifs from a long time series. Prior work has typically fit this model by multiplicative parameter updates---an approach widely considered to be suboptimal for NMF, especially in large-scale data applications. Here, we describe how to extend two popular and computationally scalable NMF algorithms---Hierarchical Alternating Least Squares (HALS) and Alternatining Nonnegative Least Squares (ANLS)---for the CNMF model. Both methods demonstrate performance advantages over multiplicative updates on large-scale synthetic and real world data.
A Provably Correct and Robust Algorithm for Convolutive Nonnegative Matrix Factorization
Jun 17, 2019



Abstract:In this paper, we propose a provably correct algorithm for convolutive nonnegative matrix factorization (CNMF) under separability assumptions. CNMF is a convolutive variant of nonnegative matrix factorization (NMF), which functions as an NMF with additional sequential structure. This model is useful in a number of applications, such as audio source separation and neural sequence identification. While a number of heuristic algorithms have been proposed to solve CNMF, to the best of our knowledge no provably correct algorithms have been developed. We present an algorithm that takes advantage of the NMF model underlying CNMF and exploits existing algorithms for separable NMF to provably find a solution under certain conditions. Our approach guarantees the solution in low noise settings, and runs in polynomial time. We illustrate its effectiveness on synthetic datasets, and on a singing bird audio sequence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge