Fast Convolutive Nonnegative Matrix Factorization Through Coordinate and Block Coordinate Updates
Paper and Code
Jun 29, 2019


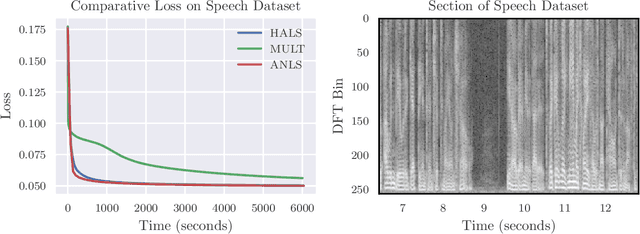
Identifying recurring patterns in high-dimensional time series data is an important problem in many scientific domains. A popular model to achieve this is convolutive nonnegative matrix factorization (CNMF), which extends classic nonnegative matrix factorization (NMF) to extract short-lived temporal motifs from a long time series. Prior work has typically fit this model by multiplicative parameter updates---an approach widely considered to be suboptimal for NMF, especially in large-scale data applications. Here, we describe how to extend two popular and computationally scalable NMF algorithms---Hierarchical Alternating Least Squares (HALS) and Alternatining Nonnegative Least Squares (ANLS)---for the CNMF model. Both methods demonstrate performance advantages over multiplicative updates on large-scale synthetic and real world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge