Differentiable Spline Approximations

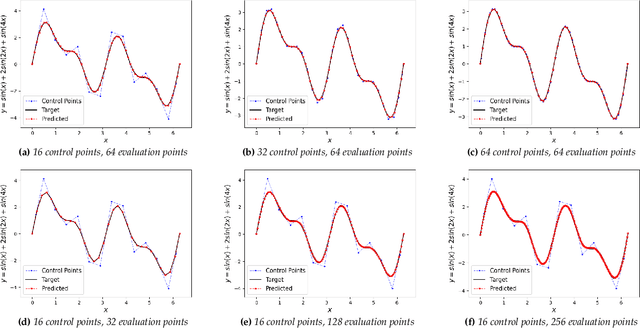
The paradigm of differentiable programming has significantly enhanced the scope of machine learning via the judicious use of gradient-based optimization. However, standard differentiable programming methods (such as autodiff) typically require that the machine learning models be differentiable, limiting their applicability. Our goal in this paper is to use a new, principled approach to extend gradient-based optimization to functions well modeled by splines, which encompass a large family of piecewise polynomial models. We derive the form of the (weak) Jacobian of such functions and show that it exhibits a block-sparse structure that can be computed implicitly and efficiently. Overall, we show that leveraging this redesigned Jacobian in the form of a differentiable "layer" in predictive models leads to improved performance in diverse applications such as image segmentation, 3D point cloud reconstruction, and finite element analysis.

NURBS-Diff: A Differentiable NURBS Layer for Machine Learning CAD Applications

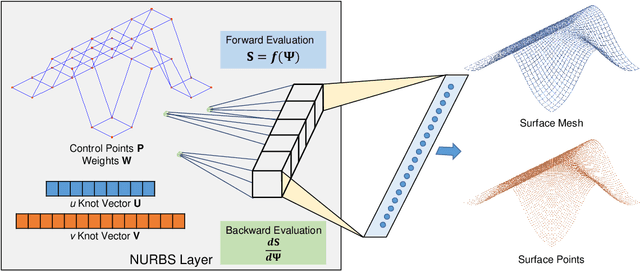
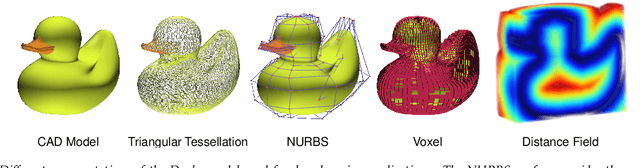
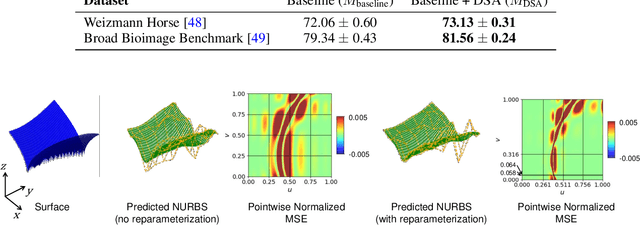
Recent deep-learning-based techniques for the reconstruction of geometries from different input representations such as images and point clouds have been instrumental in advancing research in geometric machine learning. Most of these techniques rely on a triangular mesh representation for representing the geometry, with very recent attempts in using B-splines. While Non-Uniform Rational B-splines (NURBS) are the de facto standard in the CAD industry, minimal efforts have been made to bridge the gap between deep-learning frameworks and the NURBS representation for geometry. The backbone of modern deep learning techniques is the use of a fully automatic differentiable definition for each mathematical operation to enable backpropagation of losses while training. In order to integrate the NURBS representation of CAD models with deep learning methods, we propose a differentiable NURBS layer for evaluating the curve or surface given a set of NURBS parameters. We have developed a NURBS layer defining the forward and backward pass required for automatic differentiation. Our implementation is GPU accelerated and is directly integrated with PyTorch, a popular deep learning framework. We demonstrate the efficacy of our NURBS layer by automatically incorporating it with the stochastic gradient descent algorithm and performing CAD operations such as curve or surface fitting and surface offsetting. Further, we show its utility in deep learning applications such as point cloud reconstruction and structural modeling and analysis of shell structures such as heart valves. These examples show that our layer has better performance for certain deep learning frameworks and can be directly integrated with any CAD deep-learning framework that require the use of NURBS.