xLSTM: Extended Long Short-Term Memory

In the 1990s, the constant error carousel and gating were introduced as the central ideas of the Long Short-Term Memory (LSTM). Since then, LSTMs have stood the test of time and contributed to numerous deep learning success stories, in particular they constituted the first Large Language Models (LLMs). However, the advent of the Transformer technology with parallelizable self-attention at its core marked the dawn of a new era, outpacing LSTMs at scale. We now raise a simple question: How far do we get in language modeling when scaling LSTMs to billions of parameters, leveraging the latest techniques from modern LLMs, but mitigating known limitations of LSTMs? Firstly, we introduce exponential gating with appropriate normalization and stabilization techniques. Secondly, we modify the LSTM memory structure, obtaining: (i) sLSTM with a scalar memory, a scalar update, and new memory mixing, (ii) mLSTM that is fully parallelizable with a matrix memory and a covariance update rule. Integrating these LSTM extensions into residual block backbones yields xLSTM blocks that are then residually stacked into xLSTM architectures. Exponential gating and modified memory structures boost xLSTM capabilities to perform favorably when compared to state-of-the-art Transformers and State Space Models, both in performance and scaling.

Conformal Prediction for Time Series with Modern Hopfield Networks

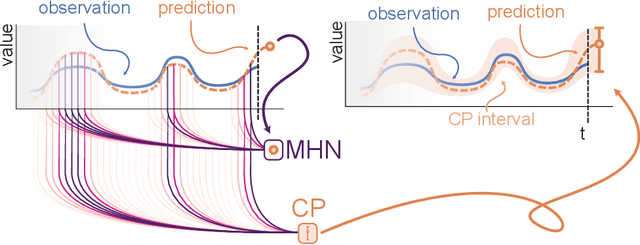
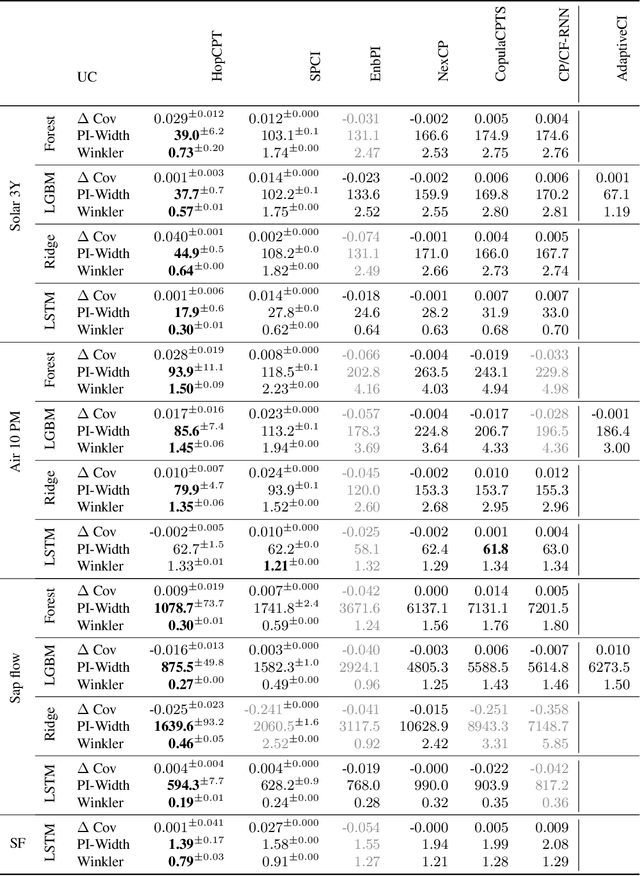
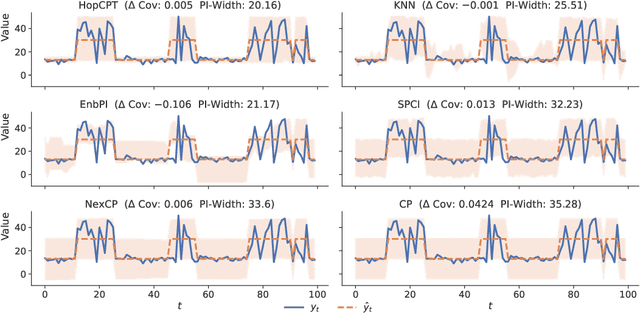
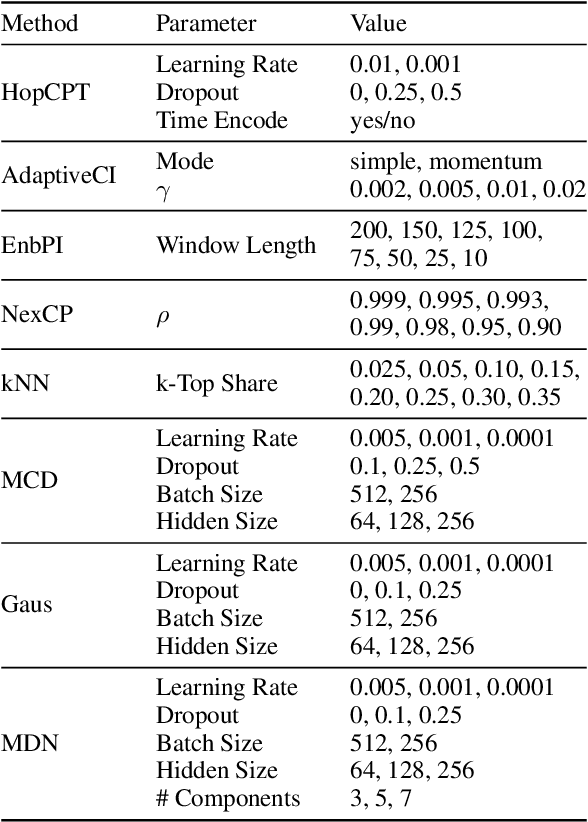
To quantify uncertainty, conformal prediction methods are gaining continuously more interest and have already been successfully applied to various domains. However, they are difficult to apply to time series as the autocorrelative structure of time series violates basic assumptions required by conformal prediction. We propose HopCPT, a novel conformal prediction approach for time series that not only copes with temporal structures but leverages them. We show that our approach is theoretically well justified for time series where temporal dependencies are present. In experiments, we demonstrate that our new approach outperforms state-of-the-art conformal prediction methods on multiple real-world time series datasets from four different domains.