Andras Lorincz
Temporal Smoothing for 3D Human Pose Estimation and Localization for Occluded People
Oct 31, 2020



Abstract:In multi-person pose estimation actors can be heavily occluded, even become fully invisible behind another person. While temporal methods can still predict a reasonable estimation for a temporarily disappeared pose using past and future frames, they exhibit large errors nevertheless. We present an energy minimization approach to generate smooth, valid trajectories in time, bridging gaps in visibility. We show that it is better than other interpolation based approaches and achieves state of the art results. In addition, we present the synthetic MuCo-Temp dataset, a temporal extension of the MuCo-3DHP dataset. Our code is made publicly available.
Multi-Person Absolute 3D Human Pose Estimation with Weak Depth Supervision
Apr 08, 2020



Abstract:In 3D human pose estimation one of the biggest problems is the lack of large, diverse datasets. This is especially true for multi-person 3D pose estimation, where, to our knowledge, there are only machine generated annotations available for training. To mitigate this issue, we introduce a network that can be trained with additional RGB-D images in a weakly supervised fashion. Due to the existence of cheap sensors, videos with depth maps are widely available, and our method can exploit a large, unannotated dataset. Our algorithm is a monocular, multi-person, absolute pose estimator. We evaluate the algorithm on several benchmarks, showing a consistent improvement in error rates. Also, our model achieves state-of-the-art results on the MuPoTS-3D dataset by a considerable margin.
Emotional Expression Classification using Time-Series Kernels
Jun 08, 2013



Abstract:Estimation of facial expressions, as spatio-temporal processes, can take advantage of kernel methods if one considers facial landmark positions and their motion in 3D space. We applied support vector classification with kernels derived from dynamic time-warping similarity measures. We achieved over 99% accuracy - measured by area under ROC curve - using only the 'motion pattern' of the PCA compressed representation of the marker point vector, the so-called shape parameters. Beyond the classification of full motion patterns, several expressions were recognized with over 90% accuracy in as few as 5-6 frames from their onset, about 200 milliseconds.
Distributed High Dimensional Information Theoretical Image Registration via Random Projections
Oct 02, 2012



Abstract:Information theoretical measures, such as entropy, mutual information, and various divergences, exhibit robust characteristics in image registration applications. However, the estimation of these quantities is computationally intensive in high dimensions. On the other hand, consistent estimation from pairwise distances of the sample points is possible, which suits random projection (RP) based low dimensional embeddings. We adapt the RP technique to this task by means of a simple ensemble method. To the best of our knowledge, this is the first distributed, RP based information theoretical image registration approach. The efficiency of the method is demonstrated through numerical examples.
Automated Word Puzzle Generation via Topic Dictionaries
Jun 02, 2012



Abstract:We propose a general method for automated word puzzle generation. Contrary to previous approaches in this novel field, the presented method does not rely on highly structured datasets obtained with serious human annotation effort: it only needs an unstructured and unannotated corpus (i.e., document collection) as input. The method builds upon two additional pillars: (i) a topic model, which induces a topic dictionary from the input corpus (examples include e.g., latent semantic analysis, group-structured dictionaries or latent Dirichlet allocation), and (ii) a semantic similarity measure of word pairs. Our method can (i) generate automatically a large number of proper word puzzles of different types, including the odd one out, choose the related word and separate the topics puzzle. (ii) It can easily create domain-specific puzzles by replacing the corpus component. (iii) It is also capable of automatically generating puzzles with parameterizable levels of difficulty suitable for, e.g., beginners or intermediate learners.
* 4 pages
Collaborative Filtering via Group-Structured Dictionary Learning
Jan 01, 2012

Abstract:Structured sparse coding and the related structured dictionary learning problems are novel research areas in machine learning. In this paper we present a new application of structured dictionary learning for collaborative filtering based recommender systems. Our extensive numerical experiments demonstrate that the presented technique outperforms its state-of-the-art competitors and has several advantages over approaches that do not put structured constraints on the dictionary elements.
* A compressed version of the paper has been accepted for publication at the 10th International Conference on Latent Variable Analysis and Source Separation (LVA/ICA 2012)
Decision Making Agent Searching for Markov Models in Near-Deterministic World
Mar 01, 2011



Abstract:Reinforcement learning has solid foundations, but becomes inefficient in partially observed (non-Markovian) environments. Thus, a learning agent -born with a representation and a policy- might wish to investigate to what extent the Markov property holds. We propose a learning architecture that utilizes combinatorial policy optimization to overcome non-Markovity and to develop efficient behaviors, which are easy to inherit, tests the Markov property of the behavioral states, and corrects against non-Markovity by running a deterministic factored Finite State Model, which can be learned. We illustrate the properties of architecture in the near deterministic Ms. Pac-Man game. We analyze the architecture from the point of view of evolutionary, individual, and social learning.
Optimistic Initialization and Greediness Lead to Polynomial Time Learning in Factored MDPs - Extended Version
Apr 21, 2009Abstract:In this paper we propose an algorithm for polynomial-time reinforcement learning in factored Markov decision processes (FMDPs). The factored optimistic initial model (FOIM) algorithm, maintains an empirical model of the FMDP in a conventional way, and always follows a greedy policy with respect to its model. The only trick of the algorithm is that the model is initialized optimistically. We prove that with suitable initialization (i) FOIM converges to the fixed point of approximate value iteration (AVI); (ii) the number of steps when the agent makes non-near-optimal decisions (with respect to the solution of AVI) is polynomial in all relevant quantities; (iii) the per-step costs of the algorithm are also polynomial. To our best knowledge, FOIM is the first algorithm with these properties. This extended version contains the rigorous proofs of the main theorem. A version of this paper appeared in ICML'09.
Factored Value Iteration Converges
Aug 13, 2008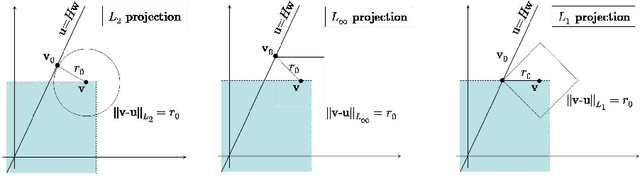
Abstract:In this paper we propose a novel algorithm, factored value iteration (FVI), for the approximate solution of factored Markov decision processes (fMDPs). The traditional approximate value iteration algorithm is modified in two ways. For one, the least-squares projection operator is modified so that it does not increase max-norm, and thus preserves convergence. The other modification is that we uniformly sample polynomially many samples from the (exponentially large) state space. This way, the complexity of our algorithm becomes polynomial in the size of the fMDP description length. We prove that the algorithm is convergent. We also derive an upper bound on the difference between our approximate solution and the optimal one, and also on the error introduced by sampling. We analyze various projection operators with respect to their computation complexity and their convergence when combined with approximate value iteration.
Online variants of the cross-entropy method
Jan 14, 2008


Abstract:The cross-entropy method is a simple but efficient method for global optimization. In this paper we provide two online variants of the basic CEM, together with a proof of convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge