Istvan Szita
Exploring compact reinforcement-learning representations with linear regression
May 09, 2012



Abstract:This paper presents a new algorithm for online linear regression whose efficiency guarantees satisfy the requirements of the KWIK (Knows What It Knows) framework. The algorithm improves on the complexity bounds of the current state-of-the-art procedure in this setting. We explore several applications of this algorithm for learning compact reinforcement-learning representations. We show that KWIK linear regression can be used to learn the reward function of a factored MDP and the probabilities of action outcomes in Stochastic STRIPS and Object Oriented MDPs, none of which have been proven to be efficiently learnable in the RL setting before. We also combine KWIK linear regression with other KWIK learners to learn larger portions of these models, including experiments on learning factored MDP transition and reward functions together.
Optimistic Initialization and Greediness Lead to Polynomial Time Learning in Factored MDPs - Extended Version
Apr 21, 2009Abstract:In this paper we propose an algorithm for polynomial-time reinforcement learning in factored Markov decision processes (FMDPs). The factored optimistic initial model (FOIM) algorithm, maintains an empirical model of the FMDP in a conventional way, and always follows a greedy policy with respect to its model. The only trick of the algorithm is that the model is initialized optimistically. We prove that with suitable initialization (i) FOIM converges to the fixed point of approximate value iteration (AVI); (ii) the number of steps when the agent makes non-near-optimal decisions (with respect to the solution of AVI) is polynomial in all relevant quantities; (iii) the per-step costs of the algorithm are also polynomial. To our best knowledge, FOIM is the first algorithm with these properties. This extended version contains the rigorous proofs of the main theorem. A version of this paper appeared in ICML'09.
Factored Value Iteration Converges
Aug 13, 2008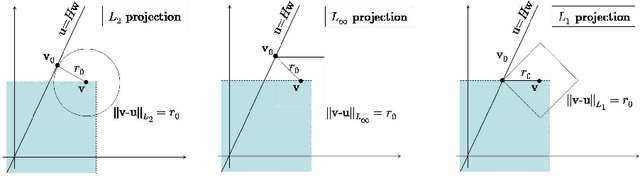
Abstract:In this paper we propose a novel algorithm, factored value iteration (FVI), for the approximate solution of factored Markov decision processes (fMDPs). The traditional approximate value iteration algorithm is modified in two ways. For one, the least-squares projection operator is modified so that it does not increase max-norm, and thus preserves convergence. The other modification is that we uniformly sample polynomially many samples from the (exponentially large) state space. This way, the complexity of our algorithm becomes polynomial in the size of the fMDP description length. We prove that the algorithm is convergent. We also derive an upper bound on the difference between our approximate solution and the optimal one, and also on the error introduced by sampling. We analyze various projection operators with respect to their computation complexity and their convergence when combined with approximate value iteration.
Online variants of the cross-entropy method
Jan 14, 2008


Abstract:The cross-entropy method is a simple but efficient method for global optimization. In this paper we provide two online variants of the basic CEM, together with a proof of convergence.
Reinforcement Learning with Linear Function Approximation and LQ control Converges
Mar 09, 2007


Abstract:Reinforcement learning is commonly used with function approximation. However, very few positive results are known about the convergence of function approximation based RL control algorithms. In this paper we show that TD(0) and Sarsa(0) with linear function approximation is convergent for a simple class of problems, where the system is linear and the costs are quadratic (the LQ control problem). Furthermore, we show that for systems with Gaussian noise and non-completely observable states (the LQG problem), the mentioned RL algorithms are still convergent, if they are combined with Kalman filtering.
Low-complexity modular policies: learning to play Pac-Man and a new framework beyond MDPs
Oct 30, 2006
Abstract:In this paper we propose a method that learns to play Pac-Man. We define a set of high-level observation and action modules. Actions are temporally extended, and multiple action modules may be in effect concurrently. A decision of the agent is represented as a rule-based policy. For learning, we apply the cross-entropy method, a recent global optimization algorithm. The learned policies reached better score than the hand-crafted policy, and neared the score of average human players. We argue that learning is successful mainly because (i) the policy space includes the combination of individual actions and thus it is sufficiently rich, (ii) the search is biased towards low-complexity policies and low complexity solutions can be found quickly if they exist. Based on these principles, we formulate a new theoretical framework, which can be found in the Appendix as supporting material.
Kalman filter control in the reinforcement learning framework
Jan 09, 2003Abstract:There is a growing interest in using Kalman-filter models in brain modelling. In turn, it is of considerable importance to make Kalman-filters amenable for reinforcement learning. In the usual formulation of optimal control it is computed off-line by solving a backward recursion. In this technical note we show that slight modification of the linear-quadratic-Gaussian Kalman-filter model allows the on-line estimation of optimal control and makes the bridge to reinforcement learning. Moreover, the learning rule for value estimation assumes a Hebbian form weighted by the error of the value estimation.
Temporal plannability by variance of the episode length
Jan 09, 2003



Abstract:Optimization of decision problems in stochastic environments is usually concerned with maximizing the probability of achieving the goal and minimizing the expected episode length. For interacting agents in time-critical applications, learning of the possibility of scheduling of subtasks (events) or the full task is an additional relevant issue. Besides, there exist highly stochastic problems where the actual trajectories show great variety from episode to episode, but completing the task takes almost the same amount of time. The identification of sub-problems of this nature may promote e.g., planning, scheduling and segmenting Markov decision processes. In this work, formulae for the average duration as well as the standard deviation of the duration of events are derived. The emerging Bellman-type equation is a simple extension of Sobel's work (1982). Methods of dynamic programming as well as methods of reinforcement learning can be applied for our extension. Computer demonstration on a toy problem serve to highlight the principle.
Searching for Plannable Domains can Speed up Reinforcement Learning
Dec 10, 2002



Abstract:Reinforcement learning (RL) involves sequential decision making in uncertain environments. The aim of the decision-making agent is to maximize the benefit of acting in its environment over an extended period of time. Finding an optimal policy in RL may be very slow. To speed up learning, one often used solution is the integration of planning, for example, Sutton's Dyna algorithm, or various other methods using macro-actions. Here we suggest to separate plannable, i.e., close to deterministic parts of the world, and focus planning efforts in this domain. A novel reinforcement learning method called plannable RL (pRL) is proposed here. pRL builds a simple model, which is used to search for macro actions. The simplicity of the model makes planning computationally inexpensive. It is shown that pRL finds an optimal policy, and that plannable macro actions found by pRL are near-optimal. In turn, it is unnecessary to try large numbers of macro actions, which enables fast learning. The utility of pRL is demonstrated by computer simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge