Unsupervised Point Cloud Registration with Self-Distillation

Rigid point cloud registration is a fundamental problem and highly relevant in robotics and autonomous driving. Nowadays deep learning methods can be trained to match a pair of point clouds, given the transformation between them. However, this training is often not scalable due to the high cost of collecting ground truth poses. Therefore, we present a self-distillation approach to learn point cloud registration in an unsupervised fashion. Here, each sample is passed to a teacher network and an augmented view is passed to a student network. The teacher includes a trainable feature extractor and a learning-free robust solver such as RANSAC. The solver forces consistency among correspondences and optimizes for the unsupervised inlier ratio, eliminating the need for ground truth labels. Our approach simplifies the training procedure by removing the need for initial hand-crafted features or consecutive point cloud frames as seen in related methods. We show that our method not only surpasses them on the RGB-D benchmark 3DMatch but also generalizes well to automotive radar, where classical features adopted by others fail. The code is available at https://github.com/boschresearch/direg .

Algebraic Relations and Triangulation of Unlabeled Image Points

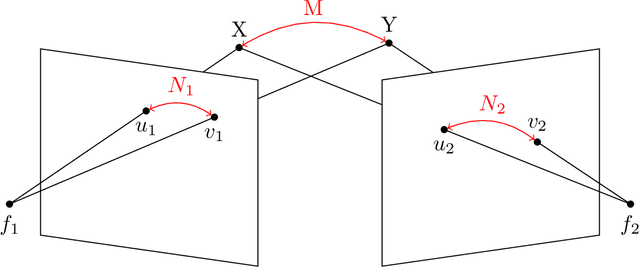
In multiview geometry when correspondences among multiple views are unknown the image points can be understood as being unlabeled. This is a common problem in computer vision. We give a novel approach to handle such a situation by regarding unlabeled point configurations as points on the Chow variety $\text{Sym}_m(\mathbb{P}^2)$. For two unlabeled points we design an algorithm that solves the triangulation problem with unknown correspondences. Further the unlabeled multiview variety $\text{Sym}_m(V_A)$ is studied.

Pictures of Combinatorial Cubes

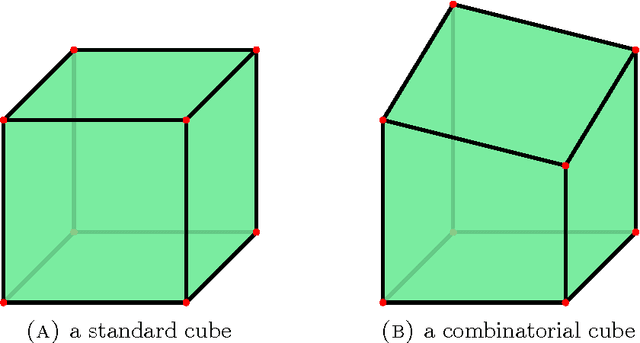
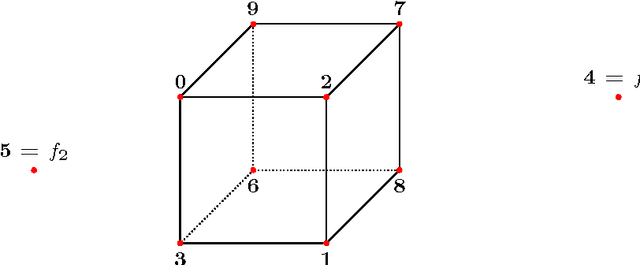
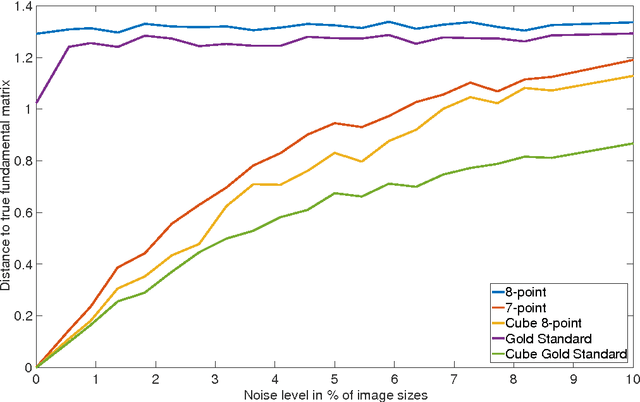
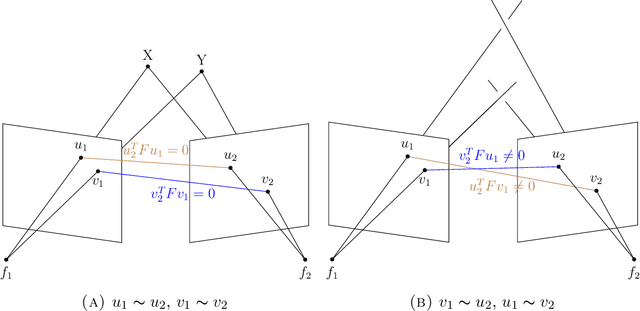
We prove that the 8-point algorithm always fails to reconstruct a unique fundamental matrix $F$ independent on the camera positions, when its input are image point configurations that are perspective projections of the vertices of a combinatorial cube in $\mathbb{R}^3$. We give an algorithm that improves the 7- and 8-point algorithm in such a pathological situation. Additionally we analyze the regions of focal point positions where a reconstruction of $F$ is possible at all, when the world points are the vertices of a combinatorial cube in $\mathbb{R}^3$.

Rigid Multiview Varieties

The multiview variety from computer vision is generalized to images by $n$ cameras of points linked by a distance constraint. The resulting five-dimensional variety lives in a product of $2n$ projective planes. We determine defining polynomial equations, and we explore generalizations of this variety to scenarios of interest in applications.