Pictures of Combinatorial Cubes
Paper and Code
Jul 20, 2017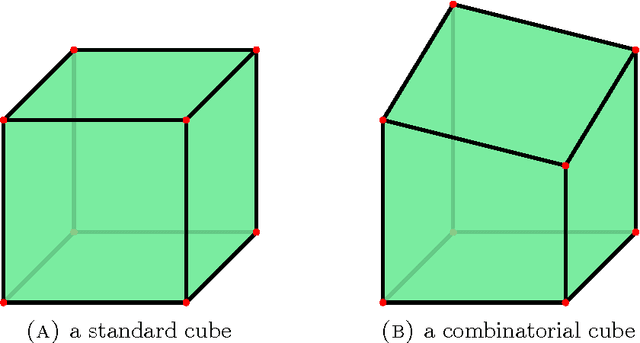
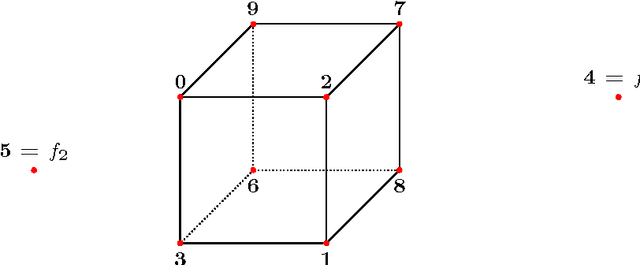

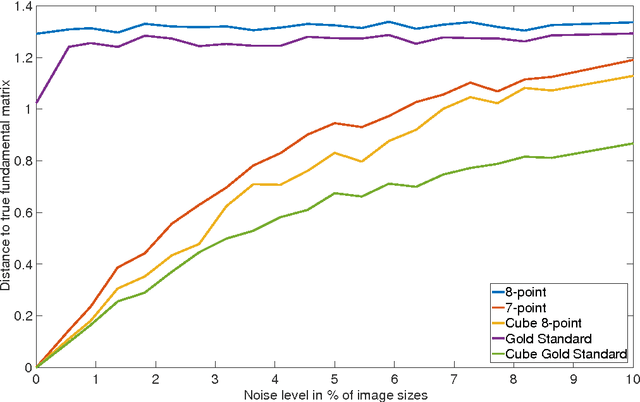
We prove that the 8-point algorithm always fails to reconstruct a unique fundamental matrix $F$ independent on the camera positions, when its input are image point configurations that are perspective projections of the vertices of a combinatorial cube in $\mathbb{R}^3$. We give an algorithm that improves the 7- and 8-point algorithm in such a pathological situation. Additionally we analyze the regions of focal point positions where a reconstruction of $F$ is possible at all, when the world points are the vertices of a combinatorial cube in $\mathbb{R}^3$.
* 12 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge