Algebraic Relations and Triangulation of Unlabeled Image Points
Paper and Code
Jul 27, 2017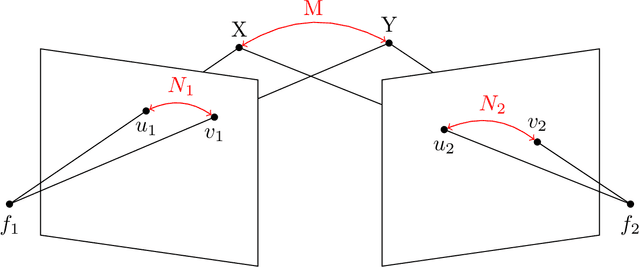

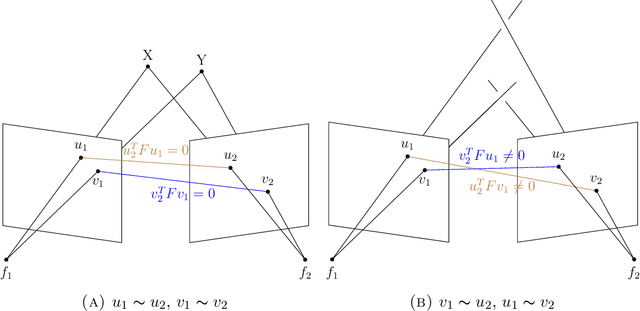

In multiview geometry when correspondences among multiple views are unknown the image points can be understood as being unlabeled. This is a common problem in computer vision. We give a novel approach to handle such a situation by regarding unlabeled point configurations as points on the Chow variety $\text{Sym}_m(\mathbb{P}^2)$. For two unlabeled points we design an algorithm that solves the triangulation problem with unknown correspondences. Further the unlabeled multiview variety $\text{Sym}_m(V_A)$ is studied.
* 17 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge